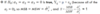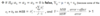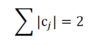ANOVA lectures 1 and 2 Flashcards
observed statistic is more extreme than critical statistic
reject Ho
p(obs|Ho) > α (i.e., p > .05), or observed statistic is not more extreme than critical statistic
the researcher would decide to retain Ho.
In ANOVA what is j?
Each level of the IV will be given a number, so j = 1 … J fixed levels
𝑛𝑗
number of participants in the j’th group
N
total number of participants in the experiment
How do you work out N?
Assume equal 𝑛𝑗 for PSYC3010, so N = 𝑛𝑗×𝐽
Between-subjects is…
= experiment where different participants have been assigned to different conditions
Fixed effects =
levels of the IV can be replicated across experiments
Null in ANOVA
𝐻0:𝜇1=𝜇2=𝜇3=⋯=𝜇𝐽
Ha in ANOVA
𝐻𝐴:not 𝐻0. Mu’s are not equal
alpha =
probability of making a Type 1 Error. Probability of falsely rejecting Ho when the true state of affairs is that Ho is True (nothing is happening) We should have retained Ho but instead we falsely rejected it.
For an independent samples t test can we draw directional conclusions?
Yes. If there is inequality between the two groups we know the direction.
One way?
An experiment with one independent variable (IV) with J levels
The General Linear Model (GLM)
Yij= μ + αj + εij. Score on the dependent variable (DV) for the ith person in the jth group (Yij)= Population grand mean (µ) + Effect parameter for group (aj) + Random error for ith person in the jth group (e)
what is mu in GLM?
everybody in the population has this
what is alpha j in GLM
effect parameters. boost we get for being in a specific group. systematic between group differences.
error in GLM
adjustment for being the person that they are. error, non systematic within group differences
Do all alpha js look the same?
No. each group has it’s own alpha j. so alpha 1, alpha 2, a3 etc. Ho is that all of the alpha js = 0. Ha is that some groups deviate from the grand mean (µ).
What about the alpha js is important for the GLM?
Sum of the alpha js have to equal zero or you have breached a requirement of the GLM, you’ve done something wrong.
What are the assumptions of error
1) Errors are independent (different people) 2) Have a mean of zero, i.e. E(εij) = 0 3) Are normally distributed 4) Has equal variance across conditions (Homogeneity of variance, or homoscedasticity) = spread of epsilons are the same across all groups.
In an experiment, all we have are the Yij observed scores, so we have to estimate these population parameters from sample data. How do we do this?
μ , αj , and εij are not usually known out ‘in the real world’. (use the sample mean Yij as an estimate of the population mean μ) Think using ‘deviations’. move the µ from left to right of the GLM equation. (Yij –Ybar) = (Ybarj-Ybar) + (Yij-Ybar).\ BUT sum of these deviations (alpha js) will always be 0, so we need to SQUARE them creating ANOVA.
What is SST conceptually?
The sum of squared deviation for each scoere (Yij) from the grand mean (Ybar).
What is SSB conceptually?
little n times the sums of sqaured deviations of each group (Ybar j) from the grand mean (Ybar)
What is SSW conceptually?
sum of squared deviation of the score (Yij) of a particular group from the mean of that particular group (Ybar j).
dfT =
N-1
dfB =
J-1
dfW =
J(n – 1) = N – J
MSW = s2 pooled =
estimate of common population variance
If Ho is true why will F ratio be close to 1?
because
If Ho is false why what will happen to F ratio?
what is nu-one and nu-two and alpha for F ratio?
𝜈1 = ‘nu-one’ = dfB
•
𝜈2 = ‘nu-two’ = dfW
•
α = Type I error rate (usually set at .05)
Four points for one way ANOVA conclusions?
- DV (levels of anxiety)
- IV (types of therapy)
- Qualifier (appears/significant)
- Statistics (observed F with dfs, p < or > .05)
E.g.:
Levels of anxiety differs significantly as a function of different therapy types, F2,9 = 11.45, p < .05.
Mean levels of anxiety following therapy was 7 (SD=2.5) for those receiving Cognitive Therapy, 9 (SD=2.2) for those receiving Behavioural Therapy, and 17 (SD=4.3) for receiving No Therapy.
•
A one-way ANOVA revealed that levels of anxiety differed significantly as a function of therapy type, F2,9 = 11.45, p < .05.
What does Tukey (Honestly Signifiant Differences) do?
This procedure tests all possible pairwise comparisons while controlling the experiment-wise Type I error rate (EER) at α = .05.
Pairwise = one this vs another. Must provide direction. Beyond this is contrasts.
For one way do you use DER, FER or EER?
Trick question they are all the same.
For a single inference,
•Decision-wise Type I error rate (DER) =
•Family-wise Type I error rate (FER) =
•Experiment-wise Type I error rate (EER).
Planned contrasts are…
formulated before looking at the data (a priori)
Post-hoc contrasts:
formulated after looking at the data
What is a contrast?
focussed question asking whether “this lot” is, on average, the same as “that lot”
linear combination of weighted means whose coefficients (i.e. weights) sum to zero
Do means have their own contrasts?
What math rule applies to contrasts?
Yes, each mean has it’s own contrast coefficients. So you have positives on one side and negatives on one side.
Mathematically, sum of contrasts must be zero.
Null hyp for contrasts
Psy = 0
If they sdon’t sum to zero you don’t have a contrast.
Psy is the sum of weighted population means. Psy equals to zero if null is true. Researcher’s hyp (Ha) is that one side is heavier.
For mean difference contrasts, standard form is defined as:
Because, Sum of the positive coefficients = +1
Sum of the negative coefficients = -1
Hand-calculations are easier if the contrast coefficients are in
integor form
integor form
whole numbers:
can you interpret integor form coefficients?
No, only standard form. Look at the means to work out what part of the contrast is higher and by how many points
what is the same in standard and integor?
SS and F are the same whether standard or integor form
v1 for a contrast is..
v2 is
always 1
dfw from the one way anova J(n-1)
All contrast conclusions must contain the
- DV, and
- Qualifier appears or sig.
- Direction of effect if it is sig.
- levels of the IV (this lot vs other lot)
- Then means (preaveraged) or the mean difference (must be on the correct standard form scale).
- Then stats.
how to work out integor
find the one with the most conditions and give them all neg 1.
Then add up the negative ones and balance them over the positive side.
0 2 -1 -1
what happens with pairwise contrasts?
in pairwise comparisons (special case) we get 00 1 -1, this is the same int vs standard.
Overall contrast conc
- descriptoves (means were…)
- one way anova conclusion (it revealed that…)
- using a DER of .05 significance level, the researcher concluded there were or were not sig differences between (this lot and that lot) (always put in means, stats)
F1, dfw from the anova) = …, p>.05 [psy symbol1]
- Other focused questions… nor did they find sig differnces between… (means)
- However they found this and that were sig different.(means!) Provide the direction if theres a difference
relation between SSB from anova and contrasts?
say we have 4 groups so 3 -1 -1 -1 = 3.
This is the same as j-1 (dfb) from the ANOVA.
Not a cosmic coincidence - this is the same as SSB.
What does 1-a mean?
Nothing systematic is happeing, because that’s the big end of bellcurve. a is the rejec part. Type 1 error rate of .05
how do you read tukey hsd output?
left to right. coparing the thing on left to all the things to it’s right. if neg, thing on right is lower. pos = higher.
