ANOVA Lectures 5 and 6

Question 1

What is EER?

Answer 1

The probability of making a type 1 error over all of the inferences or contrasts (according to k) in the experiment. The probability is no longer 5%, it’s more likley k times alpha.

Question 2

Methods of controlling the EER for contrasts: planned vs post hoc contrasts

Answer 2

For planned contrasts (formulated before looking at the data): •EER control is optional if the contrasts are orthogonal • Otherwise, researchers can use either Bonferroni or Scheffé to control the EER (typically the procedure with the smaller c.v.) Both Bon and sheffe are CONSERVATIVE. Either at alpha or a bit below alpha. For post hoc contrasts (formulated after looking at the data): • Researchers must control the EER • Only the Scheffé procedure can be used

Question 3

Why does Type I error inflate with k?

Answer 3

Number of pairwise comparisons (contrasts) = Jx(J-1) The more conditions you have in an experiment, the more likely we get extremes even though nothing systematic is happening.

Question 4

How does a researcher decide which contrasts to test before looking at the results?

Answer 4

Compare groups which can be meaningfully clustered (i.e., averaged) based on theory e.g. None vs. Any (pill, capsule, inject) Intravenous (inject) vs. Oral (pill, capsule) Pill vs. Capsule

Question 5

How does a researcher decide which contrasts to test after looking at the results?

Answer 5

(e.g. Looks like pain is lower after capsule than any of the other conditions.) So compare groups with the biggest (sample) mean difference

Question 6

Why is k ≠ 1 when doing post hoc contrasts? Why not just use the biggest mean difference and test that contrast?

Answer 6

because at least (all those other) contrasts are also implicitly tested. Even if it’s unconscious, you’ve looked at means. Probability of type 1 error is inflated with more contrasts, number of k increases quickly with number of groups. k of 10 = type 1 error rate of 50%. We don’t know what K is, so we can’t use BOnf which depends on K. K is in the formula.

Question 7

Why can’t you use bonf for post hoc?

Answer 7

We don’t know K, we have to use Sheffe.

Question 8

If null hyp for anova if true what happens to contrasts using Sheffe?

Answer 8

If you use Sheffe, they will also not be significant.

Question 9

What links sheffe to ANOVA?

Answer 9

The researcher decided to reject Ho if MSB/MSW is greater than crit F with v1 and v2 df. MSB = SSB/v1 so… this is the formula for the sheffe critical f.

Question 10

What can SS contrast be? (range)

Answer 10

Remember, for any contrast, SS contrast is a number between zero and SSB

Question 11

Why will that SS contrast = SSB for at least one contrast?

What is this contrast called?

Answer 11

Since SS contrast is between 0 and SSB,

If we reject Ho from the omnibus anova, we are saying that SSB/MSW is a number that is greater than v1 x critical F_{.05, v1, v2}.

This means we must be able to define at least one significant contrast, such that SS contrast = SSB.

This is the maximal contrast. (can only be defined post hoc.

Question 12

When is the maximal contrast defined?

Answer 12

It can only be defined post hoc because it’s based on the sum of squared deviations between each of the sample group means (Ybarj) and the sample grand mean (Ybar g).

Question 13

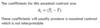
Whta happens if you have a contrast with coefficients like 7 5 -3 -9?

Answer 13

They are not interpretable because they dno’t have two groups avergaed together (mean diff cont), nor do they correspond to a trend.

Question 14

If we have looked at the means, we know the anova is significant, we want to test the contrasts, what are we using?

Answer 14

It’s post hoc so only use sheffe.

Question 15

What is the sheffe critical F table?

Answer 15

Anova F tables (normal)

Question 16

what does comfortably significant mean?

Answer 16

Obs F is at least twice the size of the crit F.

We should be able to find some sig, interpretable post hoc contrasts using the coefficients from the maximal contrast as a guide

Question 17

What is a complex contrast?

Answer 17

-1 -1 -1 3

It compars several groups. The average of two or more group means on one hand and the avergae of one or more means on the other hand.

Question 18

how do you work out how much proportio of SSB is accounted for in a contrast?

Answer 18

You divide the SScontrast by the maximal SS contrast (the SSB) to get a ratio.

e.g. Psy max SS contrast = 1640. (ss contrast 1 is 1280)

contrast 1 (psy1) accounts for 1280/1640 = 0.78 or 78% of SSB

Question 19

What happens if Contrasts are not orthogonal?

Answer 19

These SS contrasts will account for overlapping bits. If you add up the SSs they greatly exceed the SSB that is supposed to be available.

If they were orth, they would sum to SSB.

Question 20

simple contrast is

Answer 20

pairwise comparison

Question 21

If you have psy 1 of 1 0 0 -1, that is not sig, can other contrasts in the experiment be sig?

Answer 21

Even thought maximal contrast is significant, No. contrast 1 was the largest possible pairwise comparison (simple contrast)
• Contrast 1 is not significant, so no other pairwise comparison between conditions will be significant using Scheffé

So now we should be looking at other kinds of complex contrasts.

Question 22

Will SS contrast and obs F for complex contrasts be higher than simple or lower than simple ones?

Answer 22

Higher, because they’ve got more groups, and thus more power.

Think back to the formular for SS Contrast. The denominator is divided by the sum of sqaured coefficients. In standard form that will be 2. (1 0 0 -1).

For complex contrasts in standard form, the coefficients will always be a smaller number (1/3 1/3 1/3 -1) That sum of sqaured will be 1.33. Do we are dividing the SS contrast by a smaller number. So larger F value!!

Question 23

how do you create a complex contrast that is interpretable?

Answer 23

compare the groups with positive coefficients with the groups with negative coefficients?

How do you assign a grouping label to those with standard treatment and no treatment? Not interpreatble.

First you have 7 5 -3 -9.

The other method. make it (1 1 0 -2): still following the pos and neg contrasts. Drop the coefficients that are closest to zero (-3) and make it zero.

Question 24

Why would it be good to plan contrasts ahead of time

Answer 24

Because then you won’t be forced to use the highly conservative sheffe procedure. So conservative that other things won’t reach significance. Crit value will be higher than normal.

But you can have unlimited questions with bonf.

Question 26

If you have a planned contrast, no concern for controlling EER, and it is a set of mutually orthogonal, what do you use?

Answer 26

DER

Question 28

If you have concern for contorlling EER, and k is smaller than or equal to J-1, what do you use?

What if K is bigger than J-1?

Answer 28

If k is smaller than or equal to J-1, use bonferroni.

If greater than J-1, CHECK. Does sheffe or bonferroni give you a smaller F crit?

If planned always use sheffe.

Question 30

The contrast coefficients -1 -1 2 and -0.5 -0.5 1 represent the same contrast. How will ach set of contrast coefficients change?

Answer 30

Given that for any collection of group means, the group means will be the same, the contrast estimate therefore depends on the values of the contrast coefficients. In this example, for (-1 -1 2) will be twice as large as for (-0.5 -0.5 1).

Question 31

When can you interpret a contrast coefficient as a mean difference?

Answer 31

When they are in standard form - you can see in output L1, and L2 below it. The contrast estimate for L2 is the mean difference from the first contrast estimate if they are directly interpretable.

Question 32

how do you find F from a contrast output?

Answer 32

The value of F is obtained by dividing the contrast estimate by the standard error, and then squaring this result.

Question 33

two way anova questions for 2x3 (3)

Answer 33

1.

Averaged over levels of IVB, does mean DV differ as a function of IVA?
2.
Averaged over levels of IVA, does mean DV differ as a function of IVB?
3. interaction
Does the difference in mean DV between levels of IVA differ as a function of IVB?

Question 34

in two way anova what is ßk?

Answer 34

Main effect of B.

Question 35

what is an aßjk

Answer 35

interaction effect (AxB) in two way anova

Question 36

how do the effect parrameters affect the DV?

Answer 36

We don’t know what the population parameters are in real life, we estimate them.

We would use the GLM

Yijk = µ + aj + ßk + aßjk + epsilon ijk

Question 37

what happens if we have no interaction?

Answer 37

the lines are parallel, the ‘gaps’ are the same size, and effects are additive

The interaction is independent of a and b. It doesn’t change the colum and row means

Question 38

When there is an interaction

Answer 38

the lines are not parallel, the ‘gaps’ are different sizes, and the effects are ‘multiplicative’

Question 39

If there are interaction effects, we have to be careful when drawing conclusions about

Answer 39

e.g. the effects of therapy on relaxing thoughts… it depends on the type of backup received; or the effects of backup on relaxing thoughts… it depends on the type of therapy received

Question 40

Why do scores differ (from the grand mean)?

Answer 40

According to the Main Effect of A (a hat): Because the row means differ from the grand mean (Ybarj-Ybar)

According to the Main Effect of B (ßhat): Because the column means differ from the grand mean (Ybar k - Ybar)

According to the interaction effect (aßjk):

Because the cell means differ from the grand mean after removing the effects of A and B(Ybarjk−Ybar−αhat j−β
hat k)

According to the Error: Because people differ from the mean of their cell (Yijk−Ybarjk)

Question 41

Who are the 4 parameters are estimated for? How do we make them not dd to zero?

Answer 41

Each person in the experiment. The sunm of these will be zero, so to obtain an average/pooled deviations from the grand mean, we square them.

Question 42

what is F for two way anova?

Answer 42

Are the effects of these three famlilies signifianctly different from zero?

Question 43

What is FER?

Answer 43

family wise error rate. Purely between subjects design. a = .o5, but you have diff dfs.

df effect (seperate for families) and df error (same across families)

Question 44

interaction conc interpretation

Answer 44

the solid line always higher than dotted line, so differences in the DV are different across different levels of the IV. The gaps are different. Greatness/increase varies according to different levels of the IV other IV.

Question 45

What are line graohs better for with two way anova?

Answer 45

quantitative IVs.

Question 46

What is the null hyp for the Main Effect of A?

Answer 46

Do the difference or gap in DV between IV1 and IV2, does this gap differ as a function of IVA.

Null hyp: for the main effect of A, all the alpha js = 0. None of the j row means deviate from the grand mean. All the row means = grand mean.

Question 47

Null hyp for main effect of B?

Answer 47

Is the size of the gaps for B1, B2 and B3… different as a function of IVA?

All of the ßks = 0, or µk-µ = 0.