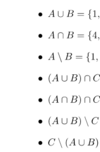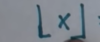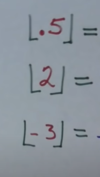Sets and functions Flashcards
What is a set?
It is a collection of objects or elements
What is the way we write sets in Ma110? use vowels as the example?>
{a,e.i,o,u}
Does order matter in sets, when comparing whether a set is the same or not?
Order does not matter ie { a,e,i,o,u} is the same as {e,i,a,u,o}
Is the set {a,a,i,e,o,u} the same as {a,e,i,o,u}?
Yes repeated elements doesnt matter.
What is the symbol we use to denote its an element of and not an element of? ?
Is a an element of {a,e,i,o,u} is b an element of {a,e,i,o,u}?
Alternatively how can we show whethera an element of {a,e,i,o,u} is b an element of {a,e,i,o,u}?
We name the set A and
What do we call a special set with no elements and how do we denote it?
1) true
2) false
3) false
4) true
5) true
6) true
7) false
8) true
9) true
What do we call, where all the elements of one set are in another set?
A subset is a set whose elements are all members of another set
What is are the symbols of subset and not a subset, ie A is a subset of B and A is not a subset of B?
1) true
2) false
3) false
4) false
5) false
6) true
7) false
8) true
9) true
There is another way of writing sets lets say we have a set
A = {a,b,c,d,e,f,g,h,i,j,k,l,m,n,o,p,q,r,s,t,u,w,x,y,z}?
This means pick all of x ( not the letter x} which is an element of A, such that x is a vowel.
This would be {a,e,i,o,u}
If this holds, what also must hold?
1) = {1,3,5,,7,9}
2) ={1,2,3,4,5}
3) = {1,2,3,4,5,6,6,7,8,9,10}
C and D are a subset of E
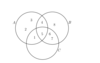
We are now going to look at set operations? what are the 4 set operations
Intersection
Union
Complement
Cartiesan products
What does the intersection of 2 sets mean e.g. A and B, whats the symbol and lets say we have 2 sets {a,e,i,o,u} and {a,e}, whats their intersection?
the set of objects that are in both A and B
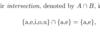
What does the intersection of A and B mean in terms of subset?
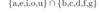
The empty set, they have no elements in common
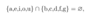
What does union of 2 sets mean?
Elements in either A or B
What is the U union for the sets
{a,e,i,o,u} U {a,e}
{a,e,i,o,u} U {a,b,c,d,e}
and what does this mean?
1) ={a,e,i,o,u}
2) = {a,b,c,d,e,i,o,u}
What does the complement of 2 sets A and B mean, whats it denoted by?
Everything in A thats not in B its denoted with a forward slash.
= {i,o,u}
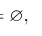
What most hold if A forward slash ( complement of) holds?
What is the cartiesan product?
Given 2 empty sets the caritsean product of A and B, is denoted by A x B, is the set of all ordered pairs, which can be mutliplied by each other.
What is {a,e,i} X {b}
What is {b} X {a,e,i}
What is {a,e,i} X {a,e,i}
Another way of representing sets are venn diagrams
Lets say we have 3 sets
A = {1,2,3,4,5} B= {4,5,6,7,8} and C = {1,5,6,7}
Represent this in a venn diagram?
Using venn diagram from previous diagram
What is the cardinality of
5
What results always holds with Cardinality?
What are natural numbers
Interger numbers
rational numbers
real numbers?
Natural numbers ( counting numbers on your hands, starts with 0,1,2,3 and up)
Integer numbers ( these are a subset of natural numbers, including their negative counter parts, e,g -1,-2,-3 etc
Rational numbers ( fill in the gaps, between the intergers, on the number line, any number that can be written as a fraction where a and b are whole numbers( subset of integers)
Real numbers ( these are numbers that cannot be written as a fraction and are irrational, they are a subset of all the above, as they include everything plus things like square root 2.)
What is a function?
It is a relation from a set of inputs to a set of possible outputs where each input related to exacly one output.
What does this mean?
this means that the function f takes elements from A and gives us elements of B.
What are A and B?
A is the domain, which is a set of all possible function inputs
B is the codomain - a set of all possible output values of a function.
Lets see we have a function f(x) = 2x
what is the domain and range?
Y F(x)
0 0
1 2
2 4
3 6
As you can see we can put any real number unto this so D = negative infinity to positive infinity
Codomain = negative infinity to positive infinity
Lets say the domain and codomain were the set of natural numbers ( counting numbers starting from 0)
would we have a function f(x) = X +1
f(x) = x-1
g(x) = 1/x)
1) yes we would have a function since every inpuy gives us an unique output, adding 1, i will always get an integer
2) no we dont have a function because every input gives us a unique output but one of these output gives us f(0) = -1, is not the codomain of natural numbers
3) we would not have a function, since there is an input 1/0 which is undefined.
What is the range of a function?
It is basically the set of all values g=f(x) ( x values
What is the domain and range of the function for the function
3x^2 + 6x -2
The range we look at the y value and domain we look at the x values
So the domain is x is an element of all the real numbers
range is all real numbers greater or equal to minus 5.
Whats the domain and range of the function f(x) = 2x + 3?
What is the domain and range for 3x^2?
What is the domain and range for x^3 +1 ?
What is the domain and range for x^4 -2 ?
What is the domain and range of e^x?
What is the domain and range for f(x) = In(x) ?
What is the domain and range for 1/x?
with the range when you divide by x, you can neva get 0, and the y values never go to 0.
What is the domain and range for f(x) = 1/x^2?
And range
What is the domain and codomain of expotentials and logarthimic functions?
What can we do with functions?
We can combine functions to make new functions
What is the relationship between expoentital and logarithmic functions?
They are the inverse of each other.
What is the sum, quotient and product rule, when combining functions to make new functions?
What is the composition of functions?
is applying one function to the results of another.
What does these two mean?
g o f means g after f
f o g means f after g
When finding an inverse of a function, what must you do?
Check if the inverse exists?
How do we know if an inverse exists?
Use this as an example?
The function must be one on one i.e. the function must give one unique output
Would the inverse exist?
we would have one-to-one, so the inverse would exist
Whats the inverse?
What is the supply function and demand function in economics?
Supply function tells us the quanitiy q, that the producers will produce given price
Demand function is the quanitity that consumers will demand given price
In equibrium supply and demand are equal.
If the supply and demand are inveritble, how can we rewrite this expression?
The price p producers charge given the quantity supplied is q
the price that the consumers will pay given that the quanitiy being demanded is q
In economic terms can we have negative prices and quanitities?
No so you always illustrate this on your graph.
: The inverse function doesn’t exist since for many values of R there is no unique q such that R = R(q). For instance we have that R(0) = R(10), R(2) = R(8), etc.
factorise and you get more than one unique solution
What does the symbol and whats the opposite?
The greatest interger less than or equal to X
( to remember, remember a floor )
there is an opposite function, which is the same but greater than or equal to X.
1) 0
2) 3
3) -3
do 4 and 5? say whether they are true or false.
4) for is correct becuase the greatest integer greater than or equal to -3.5 is -3, which is an element of an interger number.
5) this is false because the greatest interger less than or equal to -3.5 is -4, which is not an element of natural number
