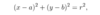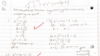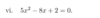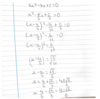Quadratic equations, parabolae and circles Flashcards
What is the form of a quadratic equation?
ax^2 + bx + c = 0
where a doesnt equal 0
Solve this quadratic equation by factorising
Factorising more difficult equations factorise 4x^2 - 4x - 3 = 0?
1) You leave the coefficient out first 4
2) you times the first number by the last to get
x^2-4x-12
3) factorise that equation
(x-6)(x+2)
4) divide by the coefficient by each unmber
(x-6/4)(x+2/4) 0
5) simplify to get ( x-3/2)(x+1/2)
6) times the 2 by the x to get
(2x-3)(2x+1)
x = 3/2 x = -1/2
Factorise 3x^2 + 5x+2
first of all times coefficient by the last number.
x^2+5x+6
(x+3)(x+2)
(x+3/3)(x+2/3)
(x+1)(x+2/3)
=(x+1)(3x+2)
Factorise 2x^2 +2x - 12
whenever, you can factor a number out do it so
2( x^2 +x -6)
then factor this s
2( x+3)(x-2)
Factorise -x^2 + x + 2
1) divide each term by -1
this equals -(x^2-x-2)
2) then factorise this keeping the negative out
- (x+1)(x-2)
Factorise - x^2+x+20
1) divide everything by -1
to get -(x^2 - x -20)
2) factorise this
- ( x -5)(x+4)
Factor
1) times the coefficient by the last number then right
x^2 + 22x+72
factor this out to get
(x+18)(x+4)
divide by the coefficient
(x+18/3)(x+4/3)
simplfily and times the x by 3
(x+6)(3x+4) =0
x = 6 x = -4/3
Now complete the square for this equation x^2+8x+18
= (x+4)^2 - 16+18
= (x+4)^2 + 2
complete the square -2x^2+ 8x+10
1) Factor out the -2
- 2[x^2+8x+10]
2) as you factor -2 be careful how you take it out
- 2[x^2-4x]+10
3) complete the square from here
- 2[(x-2)^2-4+10]
- 2(x-2)^2+6
complete the square 3x^2+9x + 5 ?
Complete the square 2x^2 +3x-7 in the form a(x+b)^2 + c
Solve 5x^2+3x-1 = 0 by completing the square?
solve 3x^2-5x=4 by completing the square?
solve -2x^2+8x+10 =0 by completing the square?
What are the rules for q/a?
With Parabolae how do you know straight away whether the parabolae has a min or a max( happy or sad face?
Demonstrate on a diagram y = -x^2 + 2x
y = x^2-4x + 3
Look at the coefficient of the equation
so if the coefficient in front of the x^2 is negative y = -x^2 + 2x + 3, then you will be sad, meaning a maximum
if the coefficient in front of the x^2 is postitive y = x^2-4x + 3, then you are happy, meaning there is a minimum.
When sketching parabolae what are the 3 things you need?
1) the y intercept
2) the x intercept
2) the turning points
How do we solve for the y and x intercepts and the turning points?
1) Y intercept is when x = 0
2) the X intercepts is when Y = 0 ( you solve by factorising
3) to find turning points you solve by completing the square
When you have a negative parabolae and when = 0 you can just reverse the equation signs.
What is the equation of a circle centered at the origin?
x^2 + y^2 = r^2
What is the equation of circle with radius r, centered at a point (a,b)?
1) CENTRE (2,7), RADIUS 10
2) CENTRE (1,-8) RADIUS 8
3) CENTRE (-1,-6) RADIUS 7
4) CENTRE (-4,5) RADIUS 2 SQUARE ROOT 5
A firm produces a quanitiy x of some good and has a profit function given by profit(x) = -x^2+24x-44
a) write the function profit(x) in a completed square form
Find the x and y intercepts
(a+b)(a-b) equals what?
a^2b^2
AND SOLVE X^2+”X+3
solve the following equations 2x^2 + 5x = 3 and by factorising and ocmpleting the square?
solve the following quadratic equations
For each of the following, complete the square and sketch the graph? y = x^2-4x+5
Sketch the graph and find the turning points?
y = -x^2-6x+6
TBH
Do i and ii
TBH
Answers:
i. The market price is 50; the revenue is 1,750. Revenue in terms of q is R = 120q − 2q 2 .
ii. Cost to produce 35 units is 820. Cost in terms of q is C = 400 + 12q.
iii. Profit when producing and selling 35 units is 930. Profit in terms of q is Π = −2q 2 + 108q − 400.
iv. Completing the square gives Π = −2(q − 27)2 + 1,058. Profit is maximised when q = 27; then the market price is p = 66.
TBA
Do question 5iii?
