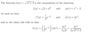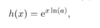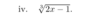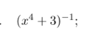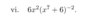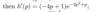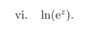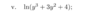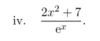Differentation more techniques

Question 1

What is the derative of f(x) = In(x)

Answer 1

1/x

Question 2

What does the power law tells us for logs?

Answer 2

Question 3

Answer 3

Question 4

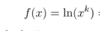
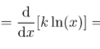
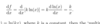
What yet dont we know how to differentatie?

Answer 4

In(x+k)

Question 5

How can we use the change of base formula to find the derative of this function?

Answer 5

Question 6

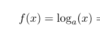
So what is the derative of this function again?

Answer 6

Question 7

Answer 7

Question 8

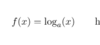
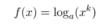
What is the derative of e^x? ( providing the base is an expoentital constant?

Answer 8

e^x

Question 9

If we have a function where the base is not an expotential constant, when what do we do?

Answer 9

1) we take logs on both side ( when a doesnt equal 1)
2) then use power rule
3) we use that the our rules of logs ( logs

Question 10

What functions can we not differentantiate without combination rules?

Answer 10

Question 11

What are the 3 ways of combining functions other than what we saw in week 5?

Answer 11

Question 12

What is the product rule?

Answer 12

f’g+fg’

Question 13

Answer 13

Question 14

Answer 14

Question 15

Answer 15

Question 16

Answer 16

Question 17

What is the quotient rule?

Answer 17

The exact same line as product rule but divide by g(x) squared

Question 18

Answer 18

Question 19

Answer 19

Question 20

Answer 20

Question 21

When do we use the chain rule?

Answer 21

when differentiating a ‘function of a function’, like f(g(x)) in general.

Question 22

What is the formula for the chain rule?

Answer 22

Question 23

Answer 23

an alternative method is use power rule so

move the 2 down to get 2(x+1) times derative in the bracket which is 1

Question 24

Answer 24

alternatively you could do:

use power rule to get 3(2x+1)^2 X the derative in the bracket 2 to get 6(2x+1)^2

Question 25

Answer 25

Question 26

Why couldnt we differentiate these functions previously??

Answer 26

because they were a funciton of a function, but now we can using the chain rule.

Question 27

Differentatite using the chain rule these functions?

Answer 27

alternative for e^kx

i know that quickly i can got e^kx X the deraitve of the power which is k as k is a constant.

same for the last function, i can do these quickly

Question 28

Differentatie this, this is a rule i need to learn

Answer 28

Question 29

How would i find the derative of this difficult function?

Answer 29

I would use the product rule but within using product rule i have to use chain rule

Question 30

Answer 30

We are going to use the product rule but the chain rule within

Question 31

Whats the derative of 2e^x?

Answer 31

2e^x

Question 32

Answer 32

f(g) = 3/(this means sqaure root g) =gx^1/3

f’(g) = 1/3g^-1/3

g(x) = 2x-1

g’(x) = 2

f’(g) x g’(x) = 2/3(2x-1)^2/3

Question 33

How can we solve this using power rules instead of chain rule?

Answer 33

• 1(x^4+3)^-2
• 1(x^4+3)^-2 X 4x^3
• 4x^3(x^4+3)^-2

then turn this into a fraction easy

Question 34

Answer 34

TBA

Question 35

Answer 35

Question 36

Answer 36

use chain rule and you should get 1

Question 37

Answer 37

Question 38

VERY HARD

Answer 38

1) Y = x^x
2) Take the natural log of both sides

InY = Inx^x( we can take expotent and move to the front)

InY = xInx

3) differentiate both sisdes with respect to x

1/y x dy/dx = ( On the RHS we use product rule) ( 1 In(x) + x times 1/x )

next step mutlple both sides by y

Question 39

Answer 39