Notes 14 constrained optimisation ( Lagrange multipliers

Question 1

In notes 11 what did we do to maxmise or minimise a quadratic function of two variables subject to a linear constraint?

Answer 1

We used completing the square method.

Question 2

What are we going to do today?

Answer 2

We are going to generalise the method of optimising functions of 2 variables in the presence of constraints that we saw in notes 11 and 13

Question 3

What is constrained optimisation with explicit constraints?

Answer 3

This is where the constraint can be rearranged to give an appropriately explicit function of one variable in terms of the other.

Question 4

Write the cosntraint so that y is an explicit function of x??

Answer 4

Question 5

When we cannot write the constraint in an appropriate explicit form, the method we will use to utlitilse this is what?

Answer 5

Lagrangean multipliers

Question 6

What is an advantage and disadvantage of lagrangean mulitpliers?

Answer 6

Question 7

What is the method of the lagrangean multipliers?

Answer 7

So basically in english you set the constraint = 0, then you form a lagrangean equation.

Find derative with respect to x, y and lander, x and y should include a lander,

then critical points is when first order derative = 0.

find the value of x and y then sub into constraint to find x and y, but when finding x you get the equation you get and equal it to the rearranged constraint to find what y is then sub to get x.

Question 8

Answer 8

Question 9

Answer 9

Question 10

What is a helpful tool when finding lagrangean mulitpliers?

Answer 10

Question 11

What are 2 applications of lagrangean multipliers are we going to use ?

Answer 11

Utility maxmisation given budget constraints

Optimisation given the relationship between the output of the firm and the costs involved in production.

Question 12

How do we convey a budget constraint in Ma110m when a consumer likes 2 goods x and y, with avaliable income avaliable?

Answer 12

Question 13

Answer 13

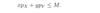
First of all identify the budget constraint and the ultiity function, and solve it like a normal lagrangean multplier.

Question 14

Now lets look at constraints with capital and labour inputs?

Answer 14

Question 15

Answer 15

Question 16

How can we find the rate of change of the maxmium value of f*(x*,y*) with a?

Answer 16

Question 17

How can we find the value of the lagrangean multiplier?

Answer 17

When we have found the value of x and y just sub them into the equations, where you took out the lagrangean, then you will find your value.

Question 18

What is the value of the lagrangean multiplier?

Answer 18

Question 19

Now we are going to look at economic interpretations of the lagrangean multiplier?

Answer 19

We can use lander* to show the marginal ulitity of money, ie to estimate the effects of a budgetary change.

Question 20

Lets say that we want to solve this?

Answer 20

You would just do the value of the lagrange multiplier times the increase in budget