More integration techniques Flashcards
How do we differentiate (2x+5)^3?
We can use the chain rule.
What the 2 more techniques we will learn with intergration?
Integration by subistution and integration by parts.
When do we use integration by subisutuition?
you need to find 1 term in the whole expression that if you take the deravative of that, it must be the same as the other term or a multiple of it.
Would we use intergration by subistution or parts?
If we look at the function in the square root and find the derartive we get 6x^2 which is a multiple of x^2.
When do we use integration by parts?
when you cannot find 1 term in the whole expression that if you take the deravative of that, it must be the same as the other term or a multiple of it.
Which method subsitution or parts?
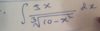
The derartive of 10 -x^2 = -2x which is a multiple of 3x
Do we use integration by subsitution or by parts?
If we take the derative of x which is 1 it is not the same as e^x or a multiple of e^x, so we use integration by parts.
Do we use integration by subsitution or by parts here?
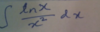
The derative of In(x) = 1/x which is not the same or mutilple as x^2 so we have to use integration by parts.
How do we work out integration by subtistution?
1) Find g ( the more complicated function)
2) differentiate with respect to x
3) find dg in terms of dx
4) find dx in terms of dg
5) then integrate by taking the starting function and put it terms of g then times dx in terms of dg.
Use integration by sub, then verify using the derived derative rule.?
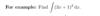
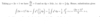
Use intergration by sub and used derived derative rule?
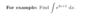
We are going to look at slightly harder integration by subsitution now? whats the difference?
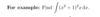
There is an extra x that is needed?
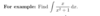
Now we turn our attention to harder integration by subistution?
Whats the key to harder integration by subistution?
We need to find dg if the dg matches the equation of the orginal, we dont need to find dx but if the equation has a mutiple of dx, then we find dg.
Now we will look at integration by parts?
What are the steps for integration by parts?
1) use product rule to differentate the harder part of the combination function and integrate the easier part,
then use the formula so it means we can integrate something easier, then integrate.
Would this require integration by sub or parts?
The extra x^2 when finding the derative is 2x which is not a mutiple of x^2. So integration by parts would be required here.
What is the last useful tool of integration we will look at?
Partial fractions
How do we solve for partial fractions?
1) Make the denominators the same then cancel them
2) solve for a by making b=0 and vice versa,
Then integrate
