Random variables Flashcards
(40 cards)
What is a random variable?
y as a variable whose values depend on outcomes of a random phenomenon or experiment
What is associated with each random variable?
A probabilitiy
Suppose we have 5 people and we measure their heights ( catogerial variable, what is the random variable?
Suppose a fair die is thrown four times and we observe two 6s, a 3 and a 1 (discrete values).What is the random variable?
The height
the score on the die
What is the random variable of a coin tossed 4 times and its sample space?

What is the sample space for a random variable?
’ which here is the set of all possible values of the random variable.
When we look at what is the likelihood, of each random variable what are we asking about?
the probability distrubtion of the random variable.
We use capital letters for what?
A random variable and lower case letters to denote a particular value of a random variable
Why does a random variable have a relative frequency interpretation?
if the experiment is repeated a very large number of times, then the probability of a given value of the random variable is equal to the number of favourable outcomes divided by the total number of experiments.
What is a probability distrubtion and what are its properties?
• A probability distribution is
: the complete set of sample space values and
the probability associated to each value
• The properties of the probability distributions are:
probabilities must be non-negative, taking values in
all values should add up to 1.
What is the probability distubtion of X?




As each value of the random variable have different probabilities e.g. lets say the random variable X is the number of workout, with taking discrete values like 1,2,3,4,5,6, what can we use to find the average amount of workouts in a week?
The expected value.
How do we find the expected value of a random variable X?
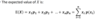
Is the expected value the same as the sample mean?
No it is different
The expected value of random variable is also referred to

Why is expected value and sample mean different?
sample mean depends on the sample we use to calculate it,so varies
Expected value is the true population mean which is known with certainty only if the whole population is sampled.
How are sample mean and expected value linked?



Tom and Bob play a game with a single fair die. Bob pays Tom an amount (in £) equal to the score of the die. In return, Tom pays Bob a fee (in £) at the start of the game. How much should the fee be so that the game is fair?

What is the expected value for a constant c
If X is a random variable, then E(cX) = ?
If a and b are constants, X and Y are random variables then E(aX + bY) = ?

What is the expected value for this g(X)



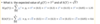


What does variance of a random variable mean?
it measures how far a set of (random) numbers are spread out from their average value