Probabilities Flashcards
Last week we said using classical probability the probabilitiy of an event is what?
P(A) = m/n
where m = the number of favourable outcomes
n = the total number N of equally likely outcomes.
What did we introduce last week in terms of sets?
In the introduction of Set Theory, we defined the union, intersection, and complement of sets.
What is the addictive law again?
If A and B are not mutually disjoint
If A and B are mutually disjoint then the 3rd term ( intersection drops out)
What is the Multiplicative law?
This is when two events A and B are independent ( no influence on each other, then
Where doesnt the multiplicative law not stand?
If the two events A and B are not independent but are dependent
• Tossing a fair coin and rolling a fair die. What is the probability that the scores are “heads” and “six”?
Use computing and abroad for proof use the multiplicative law?
So for caution if lets say we have 2 sets A and B are they are mutually exclusive ( cannot happen at the same time), whats the probability of their intersection
And if A and B are independent, what is the probability of their intersection?
What is it called when the likelihood of one event, gives information that affects the likelihood of another event?
Conditional probablitiy
What is the proper definition of Conditional probabilitiy?
The conditional probability of an event B is the probability that the event will occur given the knowledge that an event A has already occurred
What is the notation of Probability of B given A?
The probabilitiy of intersection/ whatever we are conditioning
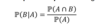
How can we simplify the conditional probability formula, supposing the 2 events are independent?
• A fair die is rolled once. Given the score is an even number, what is the probability that the score is less than 3?
We draw randomly two cards, without replacement, from a well shuffled pack. What is the probability they are both Kings?
These 2 events are dependent
What would be the total probabillity formula to get A?
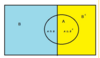
A is the whole circle so
Complete this, using home and abroad and verify this using Classical probability?
USE A TREE TO WORK IT OUT?
Draw a tree
We know the probability of P( A given B) and we know the P ( B given A) using conditional probability, rearrange this to find bayes theroem?
Given my team won, what is the probabiility that it was a sunny day?
The denoimator can be found by finding out if they won regardless whehter or not its a sunny day
Given the probability that i failed my exams, what is the probability that i didnt study?
2) If I ordered latte, what is the probability I went to “Star”?
If I ordered cappuccino, what is the probability I went to “Moon”?
In a class, the numbers of males and females are 16 and 24, respectively. Historically, 80% of males and 85% of females pass the examination. Find the probability that a student who passes the examination is female.
We use total probability law, then bayers theorem
2) If a customer defaults what is the chance there was a late payment?
Homework questions
Question 1
Anastasia Building Company (ABC) is deciding whether to submit a bid to build a new shopping centre. In the past, ABC’s main competitor, Big Building Company (BBC), has submitted bids 70% of the time. If BBC does not bid for a job, the probability ABC will get the job is 50%. If BBC bids on a job, the probability that ABC will get the job reduces to 25% due to the competition.
- If ABC gets the job, what is the probability that BBC did not bid?
ii. What is the probability that ABC will get the job?
1) We use bayers theorem so ( P bid^c/job) = P( job/bid^c)x p(bid^c)/P(job)
= 0.5 X 0.3/(0.7X0.25)+(0.3 X 0.5)
= 0.462
In a university campus, 60% of the students spend more than 25 hours a week revising, and they pass the course with probability 0.9, re-sit with probability 0.05 or fail. 30% of the students spend between 10 and 25 hours a week revising, and they pass with probability 0.7, re-sit with probability 0.2 or fail. The remaining students spend less than 10 hours revising, they pass with probability 0.5, re-sit with probability 0.2 or fail.
- If a student is selected at random after the exams, what is the probability that he/she has passed.
- If a student has not passed, what is the probability he has revised for 10-25 hours a week?
Question 2
A simple gambling game is played as follows. The gambler throws three fair coins together with one fair die and wins if the number of heads obtained in the throw of the coins is greater than or equal to the score on the die. Calculate the probability that the gambler wins.
