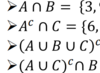Introduction to probabilities Flashcards
What does probability do?
It helps us quantify the uncertainity or likelihood of an experiment and use it in the process of decision making.
When calculating probabilities we need to define some variables, what is the letter for sample space and what is a sample space?
We define sample space as the set of all possible outcomes from that experiment.
What is the sample space of tossing a fair coin and rolling a fair dice?
What do we define an event as ?
• We define an event as a collection of outcomes from the sample space of an experiment.
An event A is what of sample space ?
It is a subset of S
What is classical probability and give examples?
where each elementary outcome is equally likely to happen.
Examples include the toss of a fair coin or the roll of a fair die
What do we denote probability of an event as?
What is the formula for classical probability?
Let be the total number of equally likely outcomes in the sample space .
Let be the number of outcomes favourable to the event of interest A.
Suppose we role 2 fair die meaning 6^2 = 36 equally outcomes?
Calculate the probability that the sum of the 2 dices = 10?
As you can see that drawing out the all the possible combinations in the 2 fair die example is quite long, so how can we find M without drawing a grid of numbers?
The combinational theory
What is Combinational theory
Helps us to count the number of outcomes, there are 3 ways to count of the number of outocmes, depending on whether the objects we are counting are in a particular order, or when the order doesnt matter.
In the combinational thoery what are the 3 ways to count the number of outcomes?
1) Factorial method
2) Permutations
3) Combinations
What is the factorial method and using this example explain it
Lets say there are 3 seats and there are and 3 people, how many many ways can we arrange the 3 people in them seats ?
It is the number of ways in which n different objects can be put in order defined as n! = n x (n-1)
In seat 1 a b or c can sit there so there are 3 scenarios, in the second chair there is only 2 people people left so 2, and in the final chair it is 1
so 3! = 3 x 2 x 1 = 6.
What are permutations, what is the formula and use the example to explain?
Lets say we have 3 seats and there is A B C D E F G people, we care about the order, how many permutations can we have in 3 spots?
It is the number of ways r objects can be chosen in order from n different objects. ( ORDER MATTERS)
Remember Permutation as positioned combination.
r = number of spots
n = number of arranged people
7! = 7 X 6 X 5 X 4 X 3 X 2 X1 /4!
the 4 factorical cancels out so we are left with 7 x 6 x 5 = 210
What is a combination, give an example and use the example below to show what a combination is, what is the formula?
A combination is a permutation, where you dont care about the order.
Lets say we have 5 books and i wont to select 3 on holiday, it doesnt matter the order, how many ways can i do this?
2 ways
1) 5 x 4 x 3 / 3 x 2 x1 = 60 / 6 = 10
2) 5!/2! 3!
= 10
What is a key example to show the difference between a permutation and a combination?
Lets say you have a storage room with a locked pad on it and the 4 numbers to unlock it is 1234. A combination would mean i could put any of them combinations e.g 3412 and it will open but a permutation wouldnt allow this.
• A group of friends are watching a play in a theatre. How many different seating arrangements can they choose from?
1) Person A can choose any of the 5 seats
2) Person B can choose any of the 4
3) Person C can choose any of the 3 remaining
4) Person D can choose any of the 2 remaining
5) Person E only has one seat remaining
5! = 5 x 4 x 3 x 2 x 1 = 120
From a group of 5 friends, only 3 can join a party. How many different combinations of friends can go to the party?
• A lottery ticket has a selection of 6 numbers from 1 to 49. During the raffle, six numbers are picked randomly. What is the probability that I have the winning ticket?
There is only one winning combination, so one favourable outcome.
The number of all possible outcomes is the number of combinations of 6 numbers out of 49, when ordering does not matter.
Five people, named A, B, C, D and E are waiting for the lift. There are seven floors in the building. Q: What is the probability that each person gets off at a different floor?
A box contains 18 light bulbs, of which two are defective. If a person selects 7 bulbs at random, without replacement, what is the probability that both defective bulbs will be selected?
Suppose an experiment is repeated independently F times, and the event A occurs f times, what can we do if we are not told how likely each experiment is?
Say we don’t know whether a coin is fair, so we dont know the likelihood of each outcome and he are interested in the event when P(A) = {H}
The coin is tossed 10 times, and event occurs 6 times.
The coin is tossed 100 times and event occurs 54 times
The coin is tossed 1000 times and event occurs 516 timess
The coin is tossed 10000 times and event occurs 5026 times
How do we know whether the coin is fair?
A factory produces smartphones.
The event of interest is B - {a smartphone is defective}
lets say 1 is defective and tested 10 times
lets say 100 smartphones are tested and 9 are defective
lets say 1000 smartphones are tested, 79 are defective, what is the probability that smartphones are defective? .
What are some notations in set theory we use for classical proabability?
Whats the difference between a set and a proabability of a set??
Show the union of 2 sets?
Show the intersection of 2 sets?
Show the complement of A ( not A)
Lets say we have a sample space = {2,3,4,5,6,7,8,9,10,11,12}
Let A be an odd total {3,5,7,9,11}
Let B be a total divisible by 3 = {3,6,9,12}
Let C be a total greater than 4 but less than 10 C={5,6,7,8,9}
Also calculate A/B ( this means given)
What does the Addictive law state about 2 events?
Lets say there is A special case is when and are disjoint, or mutually exclusive, i.e. they can not occur at the same time
What does the addicitive law say?
What does the Addictive law say about the complement of A?
There are 4 queens and 13 hearts and there are 52 cards all together
The 2 events are not mutually disjoint, they can happen at the same time.
What is the probability that a randomly chosen student does either music or sports?
What is the probability that a randomly chosen person in that small room have visited madrid or berlin?
If three fair dice are thrown, find the probability that:
a) The sum of their upturned faces is equal to 6.
If three fair dice are thrown, find the probability that:
b) The product of their upturned faces is equal to 24.
If three fair dice are thrown, find the probability that:
c) Exactly two of their upturned faces are the same.
If three fair dice are thrown, find the probability that:
d) All three of their upturned faces are the same.
If three fair dice are thrown, find the probability that:
e) All three of their upturned faces are different.
