Brainscape's Knowledge GenomeTM

Browse over 1 million classes created by top students, professors, publishers, and experts.


See full index

ST108 > Poisson, Geometric, Negative Binomial Distributions > Flashcards

Poisson, Geometric, Negative Binomial Distributions Flashcards

1
Q

What will we learn today?

A

Poisson

Poisson approximation to Binomial

Geometric

Negative Binomial

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
2
Q

What is Poisson distrubtion?

A

The Poisson distribution is used to model the number of events occurring within a given time interval.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
3
Q

What special letter do we use for the poisson distubtion?

A

Eulers number e ( expontential)

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
4
Q

What are some properties of poisson distrubtion?

A

arrivals are independent

constant rate

no more thana onen arrival at a given point of time.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
5
Q

give 2 examples of poission distubtion?

A

Machine breakdowns per uniti of time

Arrivals of buses at a stop per unit time

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
6
Q

What is the probabilitiy distibution of Possion variable? ( we are still using random variable X?

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
7
Q

What are the E(X) and Var(X) for poisson distrubtion?

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
8
Q

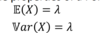
If lander is small or big what does it mean and show on a diagram with 1 and 10?

A

The Poisson distribution is skewed to the right for small lander ; the skewness becomes less as lander increases; for large values of looks symmetric.

Same for variance, the larger the lander, the more variability there is.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
9
Q

Consider a machine which breaks down, on average, 3.2 times per week, hence lander = 3.2 per week. The probability that it will break down exactly once next week is:

• The probability that it will break down exactly four times in the next two weeks

A

Be careful with lander

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
10
Q

Suppose bank customers arrive randomly on weekdays at an average of 1.5 every 3 minutes. What is the probability of:

exactly five customers in such a time?

at least four customers?

3) exactly 19 customers during an 9 minute interval
4) what is the exprected number of customers in 9 mins?

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
11
Q
  • Visitors arrive randomly at an art gallery at an average constant rate of one person every 2 minutes.
  • The door is unattended for 5 minutes. Calculate the probability that:

No visitors arrived at the gallery.

At least 3 visitors arrived.

  • Find to the nearest second, the length of time that the door had to be unattended, for there to be a probability 0.9 of no arrivals during that period.
  • Comment briefly on the assumptions of Poisson process in this context.
A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
12
Q

so write at the possion distubtion and binominal distubtion again? and there expected value?

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
13
Q

What is it possible to do with binominal distubtion and poisson distubtion?

A

• It is possible to use Poisson as an approximation to Binomial, under the following conditions

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
14
Q

What are the following assumptions we can use to use poisson to approximate the binomial?

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
15
Q

When approximaitng binominal using poisson, what is lander ?

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
16
Q

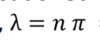
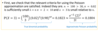
Suppose we sample 100 items at random from a production line which is providing, on average, 2% defective items. What is the probability of exactly 3 defective items in our random sample?

What do we do first? to use possion to approximate binomial?

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
17
Q

• The probability that a random page of a book has a typo is 5%. A book has 140 pages. What is the probability of exactly 8 random pages of that book have typos?

A
18
Q

From bernouli trials what are the 3 processes we have derived?

A

Binomiall

Geometric

Negative Binominal

19
Q

What is Binominal distrubtion again?

A

: we fix the number of independent repeats of the trial to , and count the number of successes, .

20
Q

What is Geometric distrubtion?

A

we stop when we get the first success, and count the number of independent Bernoulli trials needed, or ( the number of failures before you get a success in a series of Bernoulli trials.)

21
Q

Give an example of geometric disturbtion derived from bernouli ( children)?

A

A couple plans to have children until the first girl is born. What is the probability that the first child is a girl,

22
Q

What is the probability distubution of geometric distbution?

A
23
Q

What is the distubtion of the random variable X geometrically distubted and what is Var and expected value?

A
24
Q

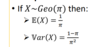
What are the proporties we have to say when working out a geometric distubution question?

A

1) there are two possible outcomes,
(2) the trials are independent, and
3) p, the probability of success, remains the same from trial to trial.

25
Q

and work out expected value?

A
26
Q
A
27
Q

What is negative binominal distrubtion?

A

we stop when we get the first successes, and count the number of independent Bernoulli trials needed, .

28
Q

So how are geometric and negative binominal linked?

A

Geometric = number of trials to get the first sucess

negative binominal = number of trials to get the rth sucess ( so number of trials to get the 2nd sucess or the 12 sucess )

29
Q

What is the probability disturbtion of negative binominal distubtion?

A

• Define X to be the number of trials until the r^th success, then the smallest number of trials is r .

30
Q

What is the difference between binominal and negative binominal distrubtion?

A

In binominal the number of trials is fixed, and we count the number of “successes”.

negative binomial distributions, the number of “successes” is fixed, and we count the number of trials needed to obtain the desired number of “successes”

31
Q

Give a question for binominal, negative binominal and geometric disturbtion they would ask for a coin?

A

Bininomial = If a coin is tossed 20 times, what is the probability heads come up exactly 4 times ?

Negative binominal = If a coin is repeadtly tossed, what is probabaility that the third time heads appears occurs on the 9th toss ?

Geometric = if a coin is repeadtly tossed, what is the probability the first time heads appears occurs on the 8th toss?

32
Q

What word will give you a hint whether it is negative binominal or binominal?

A

If it says untill ( we use negative binominal)

if it says exactly or means that then we use binominal

33
Q
A
34
Q

What is the probability that out of 15 shots he scores 3 goals?

A
35
Q

Emily drives to work each working day. She goes through sets of traffic lights that operate independently of one another. There is a probability pie= 0.3 that she stops at a given traffic light.

1) If she stops at two or less traffic lights, she has time for coffee before work. What is the probability she has time for coffee on any day?
2) What is the probability that she has the first coffee on Friday (fifth day)?
3) What is the probability that she as her third coffee on Friday (fifth day)?

A

1) we use binominal for this
2) geometric we use
3) negative binominal

36
Q

Last question before HW

• Suppose that 15% of the population are vegetarians.

What is the probability that we must interview 10 people about their diet until we find the first vegetarian?

What is the probability that we must interview 10 people about their diet until we find the third vegetarian?

What is the probability that 5 out of 35 people are vegetarians?

A
37
Q

Homework questions ?

HMRC report that 5% of taxpayers filling out the short form make serious mistakes. In a survey, 50 of these forms are chosen at random. Find the probability that at most two forms have serious mistakes. Perform the calculation:

a) using the Binomial distribution,
b) using the Poisson approximation to the binomial distribution. Discuss whether you consider the approximation is appropriate

A
38
Q

Homework question

Vehicles pass Holborn Station during weekdays at randomly at an average rate of 300 per hour. Give two reasons why we should use a Poisson distribution to describe this process.

a) Find the probability that no vehicle passes in one minute.
b) Find the probability of at least three vehicles pass in two minutes.
c) What is the expected number of vehicles passing in three minutes?

A
39
Q

Homework question continuation

Vehicles pass Holborn Station during weekdays at randomly at an average rate of 300 per hour. Give two reasons why we should use a Poisson distribution to describe this process.

d) In a 5-minute interval, find the probability that the number of cars passing is within one standard deviation from the average value.
e) Find the length of the time interval needed so that the probability that no vehicle passes during that interval is 0.90.

A
40
Q

homework question

It is believed that 25% of the population is in favour of free railway transport, in order to reduce car emissions.

a) If we take a random sample of 𝑛 = 30, what is the probability that either 4 or 5 are in favour?
b) What is the probability that we ask 5 people, until we find the 1st that is in favour?
c) What is the probability that we ask 15 people, until we find the 3rd that is in favour?
d) What is the probability that we ask 20 people, until we find the 6th that is in favour?

A
41
Q

It is believed that 25% of the population is in favour of free railway transport, in order to reduce car emissions.

How many people do we need to ask, so that the probability that at least one person is in favour is 0.8?

A
42
Q
A

ST108 (7 decks)

Brainscape helps you reach your goals faster, through stronger study habits.
© 2025 Bold Learning Solutions. Terms and Conditions