EST5_ST Flashcards
E(Yt)


Requisitos para Y(t) ser fracamente estacionário

Visualmente, observa-se estacionariedade se uma série flutua em torno de uma média fixa e se a variância da série é constante ao longo do tempo. Não obstante, são necessários testes estatísticos para verificar ou
não a estacionariedade da série.
Propriedades da Função de Autocovariância

Um processo estacionário é ergódico quando os seus momentos amostrais (médias temporais que são calculadas utilizando-se apenas uma única realização) convergem para os momentos da população.
Portanto, é possível estimar os momentos (médias estatísticas) de um processo ergódico se temos acesso a pelo menos uma realização do processo. A ergodicidade é uma propriedade mais restritiva do que a
estacionariedade, ou seja, todo processo ergódico é estacionário, mas a recíproca não é verdadeira.
O que é preciso para uma sequência ser Ruído Branco (RB)?

E(Yt) para um Modelo AR(1)

Var(Yt) para um modelo AR(1)

Autocovariância de AR(1)




E(Yt) de modelo AR(2)

p1 de um modelo AR(2)
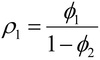


E(Yt)

Operador autorregressivo de ordem p
Se os módulos de todas as raízes da equação abaixo forem maiores do que 1 (raízes fora do círculo unitário), então a série Yt ~ AR(p) é estacionária.

A FAC do modelo AR(p) é dada por

O gráfico da FAC de um processo AR(p) é em geral constituído de uma mistura de exponenciais (devidas às raízes reais da equação característica) e senóides amortecidas (devidas aos pares de raízes complexas conjugadas da equação característica).
Var(Yt) de uma MA(q)

MA(q)

FAC do processo MA(q) é


Operador de médias móveis de ordem q

ARMA (p,q)


Operadores

Condição de Invertibilidade

Condição de Estacionariedade


Modelo de defasagem distribuída

Modelo auto-regressivo ou dinâmico

Teste de Raiz Unitária


Qual a função de transferência de FLG?

Como é a Variância em um FLG?

Como é operador Linear de um FLG?

Como detectar que um processo é invertível?

Esperança de uma Série Temporal através do FLG



Como detectar que o processo é estacionário através de FLG?

O que é e pra que serve o teste de Box-Pierce?
É um teste baseado nas autocorrelações dos resíduos estimados e serve para diagnosticar se o modelo ajustado à séries é adequado
Como detectar se a série é estacionária ou não?
É estacionária se o coeficiente autoregressivo for um número, em módulo, menor que 1
Fórmula para calcular a Covariância caso seja dado um modelo de série temporal

Uma intervenção sofrida por uma série temporal se manifesta de forma permanente ou temporária, já o tempo de duração pode ser de duração abrupta ou residual. (C ou E)?
Errado, Uma intervenção sofrida por uma série temporal se manifesta de forma abrupta ou residual, e o tempo de duração pode ser permanente ou temporária.
De forma Geral, o que é uma análise espectral de uma série temporal?
De modo geral essa análise decompõe a série temporal em componentes senoidais com coeficientes aleatórios não correlacionados.(Morettin)


