EST4_Reg Flashcards
1
Q
A
2
Q
Uma relação estatística por mais forte que ela seja, não pode estabelecer uma relação de causa e efeito; a causação de vir de fora da estatística, de outra teoria.
A
Ok
3
Q
SQTotal=n*Var(Y)
A
4
Q
Para MLS
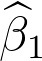
A
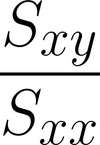
5
Q
Para MLS

A
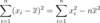
6
Q
A reta de mínimos quadrados passa pelo ponto (xbarra, ybarra)
A
7
Q
Fazer teste t com B1
A
o mais comum é testar B1=0
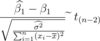
8
Q
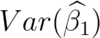
A

9
Q
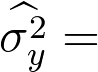
A
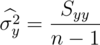
10
Q
Para MRLS

A
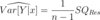
11
Q
Coeficiente de Determinação para MRLS
A
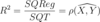
12
Q
Coeficiente de Determinação Ajustado
A
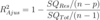
13
Q
R2
A
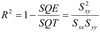
14
Q
Sxy
A
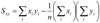
15
Q
Sxx
Syy
A
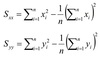
16
Q
a e b em MLS
A

17
Q
SQT, SQR e SQRes em função de y
A

18
Q
R2
A
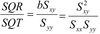
19
Q
Var(Y) = Var(erro)=σ2 para MRL
A
20
Q
Pressuposto de um MRLS
A

21
Q
O Modelo de Regressão Linear é obrigatório que apenas os parâmetros estejam na fórmula Linear
A
Ok
22
Q
SQT=SQR+SQRes
em função de Y
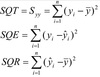
A

23
Q
Coeficiente de Determinação sem Intercepto
A
R2#r2

24
Q
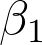
A
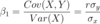
25
Var(a);Var(b); Cov(a;b)
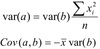
26
Percepções de MRLS

27
Fórmula alternativa para o cálculo do erro padrão residual (raiz quadrada da variância dos resíduos)
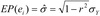
28
Teorema de Gauss-Markov
O teorema Gauss-Markov nos garante que, de todos os estimadores lineares possíveis não viesados para α e β, os estimadores de mínimos quadrados a e b, são os de menor variância. Ou seja, os estimadores a e b são os Melhores Estimadores Lineares Não Viesados (MELNV)
29
b, Var(b) e σ2

30
R2Ajustado

31
ANOVA para MRLM



