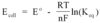Circuits
RESISTANCE
(of a material used as a resistor in a circuit)
UNITS=?
R=ρL/A
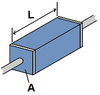
UNITS: Ω (Ohms)
- ρ=resistivity of the material
- L=length of material
- A=cross-sectional area
INTENSITY of a wave
=waves/m2
VELOCITY of a wave
V=λf
VOLTAGE in a circuit (3)
V=PE/q
V=Ed
V=Kq/r
KINETIC ENERGY
KE=½mv2
HARMONICS
FOR:
- String or pipe with MATCHING ends–
- both nodes or antinodes
- String or pipe open at ONE end –
- with one node and one antinode
λ=?
λ = 2L/n
λ = 4L/n
Snell’s Law
n1sinθ1 = n2sinθ2
Young’s Double Slit Experiment
x = λL/d
- x is the distance between fringes
- λ is the wavelength of light used
- d is the distance between the two slits
- L is the distance between the “double slit” and the final screen
TORQUE (3)
T=Fl
T=mgl
T=Frsinθ
GRAVITATIONAL PE
IN SPACE
PEgrav= - Gmm/r
PEELASTIC
PEelastic=½kx2
PEELECTRICAL (3)
PEelec=Kqq/r
PEelec=qEd
PEelec=qV
POTENTIAL ENERGY STORED IN A CAPACITOR (3)
PEcapacitor=½QV
PEcapacitor=½CV2
PEcapacitor=½Q2/C
MECHANICAL ENERGY (ME)
ME=KE+PE
WORK (2)
W=Δ ENERGY
W=Fdcosθ
RAMPS
Fm=mg (h/d)
- h is the height of the ramp
- d is the distance along its hypotenuse
LEVERS
Fm=mg( L1 / L2 )
- L1 is the lever arm for the mass
- L2 is the lever arm for the applied force
PULLEYS
Fm= mg / ( # of vertical ropes directly lifting the mass)
POWER (4)
P=ΔE/t
P=W/t
P=Fdcosθ
P=Fvcosθ
HYDRAULIC LIFTS (2)
Fm=mg (h1/h2)
Fm=mg (A1/A2)
h1=distance traveled by the large plunger
h2=distance traveled by the small plunger
A1 =cross-sectional area of the small plunger
A2 cross-sectional area of the large plunger
FORCE FOR A CONSTANT ELEC. FIELD
F=qE
FORCE FOR A POINT CHARGE ELEC. FIELD
F=Kqq/r2
<span>(Coulomb’s Law)</span>
STRENGTH OF FIELD (“E”) FOR A CONSTANT ELEC. FIELD (2)
E=F/q
E=V/d
STRENGTH OF FIELD (“E”) FOR A POINT CHARGE ELEC. FIELD
E=Kq/r2
ELEC. POTENTIAL ENERGY FOR A CONSTANT ELEC. FIELD
PEelec=qEd
ELEC. POTENTIAL ENERGY FOR A POINT CHARGE ELEC. FIELD
PEelec= (+/-) Kqq/r
VOLTAGE FOR A CONSTANT ELEC. FIELD
V=Ed
VOLTAGE FOR A POINT CHARGE ELEC. FIELD
V=Kq/r
Fmagnetic EXERTED ON A CHARGED PARTICLE,q, MOVING IN A MAGNETIC FIELD,B
F=qvBsinθ
CURRENT
I=Δq/Δt
OHM’S LAW
V=IR
ELECTRICAL POWER (3)
P=IV
P=I2R
P=V2/R
VELOCITY OF A WAVE
V=λf
THE BEAT FREQUENCY
fbeat= |f1 - f2|
THE DOPPLER EFFECT (2)
Δf/fsource= v/c
Δλ/λsource= v/c
HARMONICS FOR A STRING OR PIPE WITH MATCHING ENDS–BOTH NODES OR BOTH ANTINODES
L= nλ/2
or λ=2L/n
HARMONICS FOR A PIPE OPEN AT ONE END ONLY–ONE NODE AND ONE ANTINODE
L=nλ/4
OR λ=4L/n
ENERGY OF A PHOTON
E=hf
INDEX OF REFRACTION, “n”
n=c/v
FOCAL POINT
FOR MIRRORS ONLY
f=½r
THIN LENS EQUATION
1/p + 1/q = 1/f
MAGNIFICATION
M= -q/p
OPTICAL POWER
P= 1/f
TWO LENS SYSTEMS:
MAGNIFICATION
M=m1m2
TWO LENS SYSTEMS:
POWER
P=p1+p2
FRICTION (2)
Fk=μkmgcosθ
Fs=μsmgcosθ
THE CHARGE OF AN ELECTRON=
(in Coulombs)
-1.6 x 10-19C
THE IDEAL GAS LAW
PV=nRT
THE FUNDAMENTAL THERMODYNAMIC RELATION
ΔG=ΔH-TΔS
EQUATION RELATING KEQ TO GIBBS FREE ENERGY (2 VARIATIONS)
SPONTANEOUS IF ΔG IS (+/-)?
ΔG= -RTlnKeq
OR
Keq=e-ΔG/RT
SPONTANEOUS IF ΔG IS NEGATIVE
(“EXERGONIC”)
HEAT CAPACITY
c =ΔQ/ΔT
SPECIFIC HEAT
q=McΔT
FREEZING POINT DEPRESSION
The freezing point of a liquid is depressed when a non-volatile solute is added according to:
∆T = kfmi
kf is a constant
RAOULT’S LAW
Vapor Pressure w/ a Non-Volatile Solute =
Vapor Pressure w/ a Non-Volatile Solute = (mole fraction of the pure solvent, X)*(Vp of the pure solvent, Vp°)
Vp = XVp°
x=mole fraction of pure solvent
Vp=Vapor pressure of pure solvent
RAOULT’S LAW
TOTAL Vapor Pressure w/ a Volatile Solute =
Vptotal
= Vpsolvent + Vpsolute
( Xsolvent Vp°solvent) + (Xsolute Vp°solute)
(mole fraction, X, of solvent* Vp° of the solvent) + (mole fraction of the solute* Vp° of the solute)
OSMOTIC PRESSURE, Π
Π= iMRT
i = # of ions formed in solution
M is the solute molarity
R is the gas constant
T is the absolute temperature
BOILING POINT ELEVATION
∆T = kbmi
- where kb is a constant,
- m is MOLALITY (NOT molarity)
- i is the number of ions formed per molecule
NERNST EQUATION
Ecell = E° - (.06/n) * log ([lower]/[higher])
n=# moles of electrons transferred
Fe3+(aq)→Fe(s)
=3 e’s transferred
GIBBS FREE ENERGY
ΔG=ΔH-TΔS
GIBBS FREE ENERGY #3
in association with:
Free energy and Cell potentials
(+/-) ∆G = SPONTANEOUS/ FAVORABLE?
∆G = -nFE
n is the number of moles of electrons transferred
F is Faraday’s constant
E is the emf of the cell
NEGATIVE ∆G = SPONTANEOUS/ FAVORABLE?
^^OR A POSITIVE E°^^
GIBBS FREE ENERGY #2
in association with:
Free energy and Equilibrium Constants
(+/-) ∆G = SPONTANEOUS/ FAVORABLE?
∆G = - RTlnKeq
∆G = free energy at any moment
∆G° = standard-state free energy
R = ideal gas constant = 8.314 J/mol-K
T = temperature (Kelvin)
lnQ = natural log of the reaction quotient
(+/-) ∆G = SPONTANEOUS/ FAVORABLE?
DEPENDS ON VALUE OF Keq
SPONTANEOUS:
∆G < 0
K > 1
NON-SPONTANEOUS:
∆G > 0
K < 1
GIBBS FREE ENERGY #1
in association with:
TEMPERATURE and Free Energy
(+/-) ∆G = SPONTANEOUS/ FAVORABLE?
∆G =∆H -T∆S
NEGATIVE ∆G= SPONTANEOUS / FAVORABLE
Gases
DALTON’S LAW OF PARTIAL PRESSURES
Ptotal=P1+P2+P3…
Gases
GRAHAM’S LAW
(EFFUSION & DIFFUSION)
E1/E2=√MW2/√MW1
Density & Specific Gravity
DENSITY, ρ
ρ=m/v
Give Units–No equation here
DENSITY OF WATER=?
(2)
1000 kg/m3 OR 1.0 g/cm3
REMEMBER:
1 cm3 = 1mL
1 L H2O=1 kg
1 mL H2O=1 g
SPECIFIC GRAVITY
FOR OBJECTS FLOATING IN LIQUIDS:
WHAT IS SIGNIFICANCE OF THE FRACTION OF THE OBJECT THAT IS SUBMERGED IN WATER?
SG= ρsubstance/ρwater
ρ=density, m/v
ρwater=1 g cm3 or 1000 kg/m3
FOR OBJECTS FLOATING IN WATER:
FRACTION OF OBJECT SUBMERGED IS EQUAL TO THE SPECIFIC GRAVITY!
BUOYANT FORCE, Fbuoyant
Fbuoyant=ρvg
Fluid Pressure
GENERAL PRESSURE FORMULA
P=F/A
Fluid Pressure
FLUID PRESSURE
P=ρgh
Fluid Flow
FLOW RATE
Q=AV
A=total cross-sectional area
Fluid in motion
BERNOULLI’S EQUATION
K=P+ρgh+½ρv2
- P=random vibrational energy of the fluid molecules
- ρgh= PEgravitational per volume of the fluid
- h=height (NOT depth)
- ½ρv2 = KE per volume of moving fluid molecules
Energy Levels
WORK FUNCTION, φ
KE=E-φ
Energy Levels
ENERGY OF A PHOTON, “E”
E=hf
Chemistry
PERCENT % MASS
% MASS=
Mass of ONE element/TOTAL mass of cpd
x 100%
Equilibrium
LAW OF MASS ACTION
Keq=?
Keq=
[products]X<span> </span>/ [reactants]Y
Le Chatelier’s Principle
Qeq
MORE___ THAN ___
RXN PROCEEDS TO THE ___
MORE REACTANT THAN PRODUCT
RXN PROCEEDS TO THE RIGHT
Le Chatelier’s Principle
Q>Keq
MORE___ THAN ___
RXN PROCEEDS TO THE ___
MORE PRODUCT THAN REACTANT
RXN PROCEEDS TO THE LEFT
Evolution & Populations
HARDY-WEINBERG EQUILIBRIUM (2)
p2+2pq+q2=1
p+q=1
p is the frequency of the “A” allele in the population
q is the frequency of the “a” allele in the population
p2** represents the frequency of the **homo**zygous genotype **AA
q2** represents the frequency of the **homo**zygous genotype **aa
2pq** represents the frequency of the **hetero**zygous genotype **Aa
Ochem
“FORMAL CHARGE”
FORMAL CHARGE=
VALENCE - ASSIGNED
HÜCKEL’S RULE
4n + 2π
To exhibit aromaticity, a ring system must have exactly 4n + 2π electrons
Circuits
CAPACITANCE
C= Q/V
Waves-The dB System
INTENSITY IN dB
=10*log (I/Io)
I=intensity of wave (in W/m2)
Io=threshold of human hearing (given)
Chromatography
PAPER OR THIN LAYER CHROMATOGRAPHY (TLC)
Rf=?
Rf= DIST. TRAVELED BY COMPONENT /DIST. TRAVELED BY SOLVENT
MICHAELIS-MENTEN EQUATION
Vo= Vmax [S] / Km+[S]
MICHAELIS CONSTANT, Km
Km IS A MEASURE OF…?
Km=[S] at ½Vmax
Km= MEASURE OF AN ENZYME’S AFFINITY FOR ITS SUBSTRATE
Types of Enzyme Inhibition
LINEWEAVER-BURKE PLOTS
Y-INTERCEPT=?
1/Vmax
Types of Enzyme Inhibition
LINEWEAVER-BURKE PLOTS
X-INTERCEPT=?
-1/Km
Types of Enzyme Inhibition
LINEWEAVER-BURKE PLOTS
SLOPE=?
Km/Vmax
Circuits
CAPACITANCE**
(NOT PEcapacitor !)
How do Capacitance and PEcapacitor relate?
C=Q/V
Once solving for C, plug that into one of the 3 PEcapacitor formulas:
=½QV
=½CV2 OR
=½Q2/C
Circuits
CAPACITANCE
wrt AREA OF OVERLAP, A b/t plates
and DISTANCE, D b/t plates
C=εA/d
- C is the capacitance (Farads)
- A is the area of overlap of the two plates (m2)
- ε is the dialectric constant of the material between the plates
- for a vacuum, εr = 1
- d is the separation between the plates (m)
