Chapter 8: Dynamics of Crystal Electrons Flashcards
(14 cards)
1
Q
Semi-Classical Treatment
(3 points)
A
- Classical description of external fields
-
Quantum description of electron dynamics
- TDSE
2
Q
Semi-Classical Motion of Electron
(Velocity, Acceleration Equations)
A
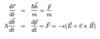
3
Q
Semi-Classical Wave Function
(3 points)
A
- Change from Block waves → superposition of Bloch waves
- εn(k) ≡ dispersion
- ∆k small compared to Brillouin zone
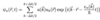
4
Q
Semi-Classical Momentum
(3 points)
A
- Well-defined momentum → delocalization in x-direction
- Propagation from group velocity
- Different ω(k) propagate at different rates → broadening over time

5
Q
Basics of Semi-Classical Model
(3 points)
A
- Describes motion of band electrons in presence of external fields
- Assign each electron postion r, wavenumber k, band index n (dispersion εn(k) known)
- External forces cause parameters to change according to dynamics rules
6
Q
Semi-Classical Model: Dynamics Rules
(6 points)
A
- Band index constant n
- Equations of motion (see below)
- Effective mass (own flash cards)
- Momentum only conserved up to G
- Thermal equilibrium, electron states in nth-band determined by Fermi statistics
- D(k)F(εn, T)d3k
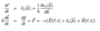
7
Q
Semi-Classical Model: Effective Mass
A
- time-derivative of group velocity (see below)
- Can read-off inverse of effective mass, because a = m-1F
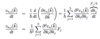
8
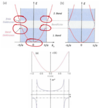
Q
Effective Mass Importance
(3 points)
A
- Can describe electrion in band as free electron with effective mass
- Most useful in upper-valance, and lower-conduction, band where bands approximation parabolic ε(k) = εo ± \hbar2/(2m)(kx2 + ky2 + kz2 )
- Effective mass inversely proportional to concavity of ε(k)
9
Q
Motion of Crystal Electrons: Filled Bands
(2 points)
A
- No electric current
- No heat current
10
Q
Motion of Crystal Electrons: Partially Filled Bands
(7 points)
A
- Electric Field
- Non-zero current
- Periodic potential leads to Bloch Oscillations
- __Magnetic field
- Electrons move on surfaces of constant energy with trajectories perpendicular to B-Field
- Open, and closed, trajectories
- Cyclotron frequency of closed trajectory ωc = eB/m
- Electrons move on surfaces of constant energy with trajectories perpendicular to B-Field
11
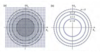
Q
Quantization of Electron Paths in B-Field
(6 points)
A
- Solving Schrodingers equation yields results similar to quantum harmonic oscillator
- Energy eigenvalues (see below)
- E = (n + 1/2)(\hbar)ωc + (\hbar kz)2/(2m)
- Quantization of trajectories in xy-plane leads to Landau levels
- Area between adjacent circles constant and ∆S ∝ B
- Number of electrons per level finite and p ∝ B
12
Q
De Haas-van Alphen Effect
(Overview)
A
- Oscillation of magnetization of metals as function of high B-field and low temperature
13
Q
De Haas-van Alphen Effect
(Assumptions: 6 points)
A
- N electrons
- |B| > 0
- Landau level S fully filed and S+1 partially filled
- EF ∈ S+1
- Increasing B increases EF, because ES+1 ∝ B
- Degeneracy of S, pS ∝ B, so eventually S+1 becomes empty and EF ∈ S
14
Q
De Haas-van Alphen Effect
(Take-Away)
A
- Can see oscilation of Fermi energy in U vs 1/B