Chapter 4: Dynamics of Crystal Lattices Flashcards
Lattice Dynamics
(4 points)
- Lattice is not rigid
- Lattice vibrations due to finite temperature
- Even at T = 0, quantum fluctuations are possible
- Approximations are needed to explain lattice dynamics
Adiabatic Approximation
(Assumptions: 4 points)
- Electrons instantaneously follow nuclei
- Follows from Newton’s 3rd Law
- me/mp = 1/1836
- Heavy nuclei oscillate slower than electrons
- Follows from Newton’s 3rd Law
Adiabatic Approximation
(Take-Away: 2 points)
- Can track motion of ion first and then electron
- Energy of electron corresponds to rigid lattice with momentary position of nuclei
Harmonic Approximation
(Assumptions: 6 points)
- Displacement from equlibrium small
- Ion-ion potential considered harmonic
- Comes trom Taylor expansion of potential between ions φ(rn − rm)
- First term: Equilibrium energy → set to zero
- Second term: Forces exerted by all other atoms → zero at equilibrium
- Third term: Second derivative of potential → generalized Hooke’s Law
- Comes trom Taylor expansion of potential between ions φ(rn − rm)
Harmonic Approximation
(Take-Away: 3 points)
- Can consider crystal as masses conneced to all other masses by springs
- Usually only consider nearest-neighbor interactions
- Valid because of Coulomb interactions
Source of Lattice Vibrations
Thermal fluctuations
Dispersion Relation
(3 points)
- Relates the wavenumber k to its frequency ω(k)
- Derive from solving equation of motion
- N unit cells with r’ atoms → 3r’N differential equations
Transverse vs Longitudinal Vibrations
(2 points)
- transverse → displacement perpendicular to propagation
- longitudinal → displacement parallel to propagation
Monoatomic Dispersion Derivation
(Assumptions: 5 points)
- Pure longitudinal wave in 1D
- Force exerted in plane un by atoms in plane un+p
- Harmonic approximation
- Ansatz: un+p = A ei(qpa-ωt)
- Nearest-neighbor interactions only
Monoatomic Dispersion Derivation
(Results)
Dispersion relation:
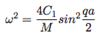
Monoatomic Dispersion Relation
(Properties: 4 points)
- Periodic
- Symmetric
- 2πn/a is length of reciprocal lattice vector
- Domain −π/a ≤ q ≤ π/a → first Brillouin zone
Group Velocity
Velocity of wave packet propagation through lattice
Monoatomic Group Velocity
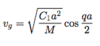
Monoatomic Dispersion Extreme Cases
(9 points)
- q = π/a → vg = 0 → standing wave
- Edge of first Brillouin Zone
- Maximum dispersion ωmax
-
qa << 1 → long wavelength
- dispersion approximately linear
- vg = constant
- Velocity of longitudinal sound wave
- Near Γ-point
- Crystal lattice considered continuum
First Brillouin Zone and Dispersion Relation
(3 points)
-
ω(q) has periodicity q = 2π/a
- Shortest possible reciprocal lattice vector
- Can just consider dispersion in first Brillouin Zone
Diatomic Dispersion Relation
(Assumptions: 5 points)
- Diatomic basis with mass M1, M2
- Each plane contains one species
- 1D longitudinal wave
- Nearest-neighbor interactions only
- Same coupling constant C
Diatomic Dispersion Relation
(Take-Away: 4 points)
- DIspersion relation (see below)
- Two branches
- Optical (+): Atoms oscillate out of phase
- Acoustic (-): Atoms oscillate in-phase
Lattice Vibrations in 3D & Branches
Consider r’ atoms per unit cell
- 3 acoustic branches
- 3r’-3 optical branches
- 3r’ total branches
Density of Phonons
(Overview: 5 points)
- Finite crystal leads to restrictions of allowable q
- λ > L ( or q < 2π/L) not possible
- Finite number of eigenfrequencies
- N masses ≤ 3N eigenfrequencies
- Depends on boundary conditions
- N masses ≤ 3N eigenfrequencies
Fixed Boundary Conditions - 1D
(Assumptions: 5 points)
- Atomic position: xn = na for n = 0,…,N
- Displacement: un
- Chain length: L = Na
- Number of atoms: N+1
- Ansatz: un = A1ei(qna - ωt) + A2e-i(qna + ωt)
Fixed Boundary Conditions - 1D
(Boundary Conditions)
- un(0) = uL(Na) = 0
Fixed Boundary Conditions - 1D
(Take-Away)
- N - 1 oscillatory modes
Periodic Boundary Conditions - 1D
(Assumptions: 5 points)
- Atomic position: xn = na for n = 0,…,N
- Displacement: un
- Chain length: L = Na
- Number of atoms: N+1
- Ansatz: un = Aei(qRn - ωt); Rn = na
Periodic Boundary Conditions - 1D
(Boundary Conditions)
- un = un+N
Periodic Boundary Conditions - 1D
(Take-Away: 4 points)
- N oscillatory modes
- For r-atom basis
- rN oscillatory modes
- N Bravais lattice points
Density of Phonon States
the number of q-vectors per volume element in momentum space
Density of Phonons in 1D Momentum Space
Periodic Boundary Conditions - 3D
(Assumptions: 7 points)
- Crystal with lattice vectors a1, a2, a3
- Crystal dimension N1a1, N2a2, N3a3
- Number of lattice points N = N1N2N3
- Monoatomic basis
- Harmonic oscilations
- Ansatz: u(R) = Aei(<strong>qR</strong>-ωt)
- q is reciprocal lattice vector
Periodic Boundary Conditions - 3D
(Boundary Conditions)
- u(R) = u(R + Niai) for i = 1,2,3
Periodic Boundary Conditions - 3D
(Take-Away: 4 points)
- 3N oscillation modes
- For r-atom basis
- 3rN modes
- N Bravais lattice points
Density of Phonon States in 3D Momentum Space
Density of Phonons in 3D Frequency Space
Properties of Phonons
(4 points)
- Energy: E = (h-bar)ω
- Momentum: p = (h-bar)q
- ω,q related via dispersion relation
- High amplitude of classic oscillation means larger number of phonons
Phonon Momentum
(4 points)
- Momentum only conserved up to reciprocal lattice vector G
- (h-bar)k’ = (h-bar)k + G
- Inelastic scattering conservation (see attached)
- Phonons do not carry true momentum, but they behave as if they carry quasi-momentum (h-bar)q in scattering process
