Chapter 7: Band Theory

Question 1

Band Theory

(Motivation)

Answer 1

• Free electron gas model does not explain why some materials are metals and others are insulators

Question 2

Band Theory

(Assumptions: 3 points)

Answer 2

• No electron-electron interactions
• Electrons interact with periodic crystal lattice
  
  • Main difference between free electron gas

Question 3

Bloch’s Theorem

Answer 3

The energy eigenstates of an electron in a crystal can be written as a Bloch wave (see below), with u(r) having the same periodicity as the lattice

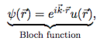
Question 4

Bloch’s Theorem

(Assumptions)

Answer 4

• Periodic boundary conditions

Question 5

Bloch’s Theorem

(Take-Away)

Answer 5

• k=2πn/(Na) for n = 0, 1, 2, …, N-1

Question 6

Kronig-Penney Model

(Assumptions: 5 points)

Answer 6

• Finite potential barriers with height V_o and width b
• Solve by plugging Bloch function into Schrodinger’s equation
  
  • Case 1: 0 < x < a :
    
    • ​Wave propagates in both directions
  • Case 2: a < x < b :
    
    • Attenuation of wave in barrier

Question 7

Kronig-Penney Model

(Boundary Conditions: 2 points)

Answer 7

• u_(a)(a) = u_(b)(-b)
• u’_(a)(a) = u’_(b)(-b)

Question 8

Kronig-Penney Model

(δ-function Barriers: 3 points)

Answer 8

• V → ∞ and b → 0 at same rate
  
  • Area of barrier remains constant
• Introduce P = lim _{b→0 β→∞} β²ab/2

Question 9

Kronig-Penney Model

(Take-Away: 4 points)

Answer 9

• Dispersion relation (see below)
• Solutions only exist for |L| ≤ 1
• Leads to bands within dispersion relation and band gaps, with shape dependent on P
  
  • Band gaps due to Bragg reflection at Brillouin Zone boundary

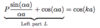
Question 10

Kronig-Penney Model

(Graphs: 4 points)

Answer 10

• Left side of dispersion relation (top)
• Dispersion relation results (bottom)
  
  • Blue: P = 0 ⇒ free electron
  • Red: P → ∞ ⇒ infinite potential well