Chapter 5: Thermal Properties of Crystals

Question 1

Thermal Properties of Crystals

(3 points)

Answer 1

• Specific heat
• Thermal expansion
• Thermal conductivity

Question 2

Specific Heat

Answer 2

The amount of energy needed to raise the temperature of a substance by one degree

Question 3

First law of Thermodynamics

Answer 3

dQ = dU - dW = dU + pdV

Question 4

Specific Heat at Constant Pressure and Volume

(3 points)

Answer 4

• C_P - C_V = TVα_V²B
  
  • α_V ≡ thermal expansion coefficient
  • B ≡ bulk elastic modulus

Question 5

Specific Heat: Classical Treatment

(Assumptions: 2 points)

Answer 5

• 3r’N independent vibration modes
• Equipartition theorem states each mode contant k_BT/2 potential and kinetic energy each

Question 6

Specific Heat: Classical Treatment

(Take-Away: 3 points)

Answer 6

• Dulong-Petit specific heat
  
  • C_V = 3r’Nk_B
• Only valid for high T

Question 7

Specific Heat: Quantum Treatment

(Assumptions: 2 points)

Answer 7

• 3N harmonic oscillators
• Temperature T

Question 8

Specific Heat: Quantum Treatment

(Take-Away: 6 points)

Answer 8

• Expectation value of internal energy (see below)
• For r-atom basis
  
  • 3N → 3rN
  • ω → ω_qr
  • < n > → < n_qr >
  • <U > → (see below)

Question 9

Specific Heat: Einstein Approximation

(Assumptions)

Answer 9

• All modes vibrate with same frequency ω_E

Question 10

Specific Heat: Einstein Approximation

(Take-Away: 3 points)

Answer 10

• Θ_E = (h-bar)ω_E/k_B → Einstein temperature
• Works well for 200 K < T < 1300 K
• Good approximation when optical branches dominate

Question 11

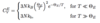
Specific Heat: Debye Approximation

(Assumptions: 7 points)

Answer 11

• All 3 phonon branches have linear dispersion ω_i = v_iq
• Integrating over first Brillouin Zone equivalent to integrating overr sphere of radius q_D
  
  • ​Each q-state occupies volume (2π/L)³
  • Each branch has N states
    
    • q_D = (6π² N/V)^1/3
  • Debye frequency ω_D = v_iq_D
  • Density of states in frequency space Z(ω) = (V/2π²v_i²) ω²

Question 12

Specific Heat: Debye Approximation

(Take-Away: 5 points)

Answer 12

• Θ_D = (h-bar)ω_D/k_B → Debye temperature
  
  • Defines limit between classical and quantum treatment
  • Measure of maximum phonon frequency
• C_V ∝ T³
  
  • Agrees with experiment for low T

Question 13

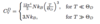
Specific Heat Comparison Graph

Answer 13

Question 14

Number of Phonons

Answer 14

Question 15

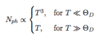
Anharmonic Effects

(Harmonic Short-Comings: 4 points)

Answer 15

• No thermal expansion
• Elastic constant independent of P,T
• C_P = C_V with C_P constant for T > Θ_D
• No phonon interactions

Question 16

Anharmonic Potential

(Assumptions)

Answer 16

• Comes from considering more terms of Taylor expansion

Question 17

Anharmonic Potential

(Take-Away: 4 points)

Answer 17

• Anharmonic coupling (3 phonon process)
  
  • Two phonons create another one
  • One phonon decays into two phonons
• Without anharmonic coupling, solid would never cool down

Question 18

Anharmonic Potential: Conservation Laws

(4 points)

Answer 18

• Relaxed conservation laws (see below)
• Normal (n-)Process: G = 0; stays in first Brillouin Zone
• Umklapp (u-)Process: Choose G so that q₃ is in first Brillouin Zone
  
  • Momenteum quasi-conserved, because some momentum transferred to lattice

Question 19

Thermal Expansion

Answer 19

• Solids change length, volume when T is varied

Question 20

Mean Particle Displacement

(3 points)

Answer 20

• For 1D oscillator:
  
  • Harmonic Oscillator: < u > = 0
  • Anharmonic Oscillator: < u > = 3b/(4a²)k_BT**​

Question 21

Thermal Conductivity

(Overview: 5 points)

Answer 21

• Heat is transported by phonons and electrons
  
  • Electronic constribution dominates in metals
  • Crystalline insulators good thermal conductors at low T
• Non-equilibrium quantity
  
  • Requires temperature gradient

Question 22

Thermal Conductivity

(Definition)

Answer 22

• Expression for K can be derived from Kinetic Gas Theory

Question 23

Kinetic Gas Theory

(Assumptions: 4 points)

Answer 23

• Phonons has of quasi-particles
• Average particle current in +x-direction j_x = n< |v_x| >/2
• Every particle delivers thermal energy ∆Q = C’_V ∆T
• Mean free-path l

Question 24

Kinetic Gas Theory

(Take-Away: 3 points)

Answer 24

• Obvious T dependence
  
  • C_V = C_V(T)
  • l = l(T)

Question 25

Temperature-Dependence of K: Scattering Processes

(Dominant Scattering Processes: 2 points)

Answer 25

• phonon-phonon scattering
• defect, surface scattering

Question 26

Matthiessen’s Rule

Answer 26

In case of several, independent scattering mechanisms, total scattering time τ can be determined by

Question 27

Phonon-Phonon Scattering

(2 points)

Answer 27

• n-processes: Do not contribute to heat resistance
• u-processes: Loss of phonon momentum leads to heat resistance

Question 28

Defect Scattering Contribution to K

(2 points)

Answer 28

• Probability proportional to defect density n_D and scattering cross-section σ
• Contribution to K is independent of T

Question 29

Temperature Dependence of K Results

Answer 29