Chapter 7: Radiation and Matter

Question 1

Interaction btwn Radiation and Matter

(Hamiltonian)

Answer 1

• Decompose into interacting and non-interacting parts
• NOTE: Assumes Coulomb gauge [A,p]=0

Question 2

Interaction btwn Radiation and Matter

(Hilbert Space)

Answer 2

Only H_int acts on both spaces

Question 3

Time-Dependent Perturbation Theory

(Hamiltonian)

Answer 3

• H₀ is time-independent and complete eigenbasis is known
• H’(t) is small

Question 4

Interaction Picture

(Overview)

Answer 4

• Intermediary picture between Schrödinger and Heisenberg
• Expectation values are invariant

Question 5

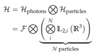
Dirac Time-Evolution Operators

Answer 5

Expand U_D(t) to get approximations

Question 6

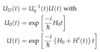
Interaction Picture

(Wavefunction)

Answer 6

Question 7

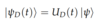
Interaction Picture

(Operators)

Answer 7

Question 8

Interaction Picture

(Schrödinger Equation)

Answer 8

Question 9

Interaction Picture

(Summary)

Answer 9

• States evolve under interaction Hamiltonian
• Operators evolve under non-interacting Hamiltonian

Question 10

Fermi’s Golden Rule

(Transition Probability)

Answer 10

Gives probability for the transition between two states due to external excitation

Question 11

Fermi’s Golden Rule

(Rate Equation)

Answer 11

Question 12

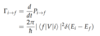
Fermi’s Golden Rule

(Rate Equation [Multiple Final States])

Answer 12

ρ(E_i) ≡ density of state at E_i

Question 13

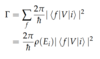
Hydrogen Atom in Radiation Field

(Assumptions)

Answer 13

• Hailtonian: H = H₀ + H’= (H_part + H_em) + H_int
• Initial state:
  
  • | i > ≡ | a > | n_<em>kλ</em> >
  • E_i = E_a + (hbar) ω_kλn_kλ
• _​Final state:
  
  • | f > ≡ | b > | n_<em>kλ</em> + 1 >
  • E_f = E_b + (hbar) ω_kλ(n_kλ+1) = E_i ​

Question 14

Hydrogen Atom in Radiation Field

(Take-Away)

Answer 14

• δ(E_i − E_f) gives that emitted photon must have energy equal to energy difference of final and initial energies
• Transition rate yield expressions for stimulated/sponstaneous emission and stimulated absorptions
  
  • n_kλ = 0 → spontaneous emission
  • n_kλ > 0 → stimulated emission/absorption

Question 15

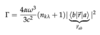
Hydrogen Atom in Radiation Field

(Notes)

Answer 15

• ω³/c² ∈ field
• r_ab ∈ atom
• fine structure constant α ≡ coupling strength between matter and radiation

Question 16

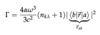
Hydrogen Atom in Radiation Field

(Selection Rules)

Answer 16

• Evaluating dipole overlap term r_{<em>ab </em>}leads to selection rules
• Matrix element vanishes unless ∆l = ±1, ∆m = ±1, 0