Chapter 2: Angular Momentum and Spin Flashcards
(19 cards)
Symmetries
- Symmetries are represented by unitary operators
- conserve scalar product and normalization
- conserve energy → commute with Hamiltonian [H,U] = 0
- NOTE: except, time-revresal symmetry is anti-unitary
- Each symmetry corresponds to some conserved physical quanitity

Types of Symmetries and
Corresponding Conserved Quantity
- Translational ⇐⇒ linear Linear momentum
- Rotational ⇐⇒ Angular momentum
Translational Symmetry
- U<b>a</b> translates by a
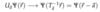
Rotational Symmetry
- U<strong>ω </strong>rotates about axis ω through angle |ω|
- R<strong>ω </strong>is representation of rotation in real-space
- R<em><strong>ω</strong></em> ∈ SO(3) = {3 × 3 matrix : A−1 = AT , detA = 1}
- Rotations do not commute
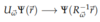
Generator of Translation
momentum operator
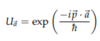
Translation Commutation

Generator of Rotation
angular momentum operator
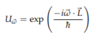
Rotation (and Angular Momentum) Commutators
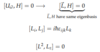
Angular Momentum
(Eigenstates and Eigenvalues)
NOTE: l is integer or half-integer
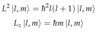
Angular Momentum
(Lowering and Raising Operators)
- In analogy to harmonic oscillator, introduce lowering and raising operators
- λ± gives mmin = −l
- For fixed l, HL = {| l, m> : m = −l, . . . , l} is irreducible subspace with representation DL on HL
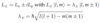
Spin
(Motivation)
- Up to now, only 1D wavefunction
- Consider how rotations act on vector wavefunctions
Generator of Infinitesimal Rotation of Vector Wavefunction
- For |ω| → 0
- Spin is internal degree of freedom that has special consideration under rotation

Spin
(Eigenstates and Eigenvalues)
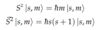
Hydrogen Atom
(Hilbert Space)
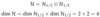
Hydrogen Atom
(Natural Basis)

Spin
(Lowering and Rasiing Operators)
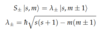
Addition of Angular Momentum Generalization
(Overview)
- Consider J = J1 + J2
- Basis & Dimension
- New basis |j1j2jm> characters by eigens states of J2, Jz for J = J1 + J2
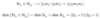
Addition of Angular Momentum Generalization
(Allowable j values)
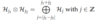
Addition of Angular Momentum Generalization
(General Basis Transformation)
- given by Glesh-Gordon Coefficients



