Chapter 1: Review

Question 1

Time-Dependent Schrödinger Equation

Answer 1

Question 2

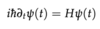
Time-Independent Schrödinger Equation

Answer 2

Question 3

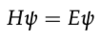
Wavefunction and Hilbert Space

Answer 3

• ψ ∈ H Hilbert Space
  
  • _​_linear, complex vector space
  • closed under addition and multiplication
  • complete
  • scalar/inner product
  • can be infinite but with countable set of basis states

Question 4

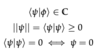
Definition of Hermitian

Answer 4

Question 5

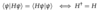
Hamiltonian Operator H

Answer 5

• H is linear, operator of observable

Question 6

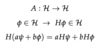
Hamiltonian for Particle in 3D with no Magnetic Field

Answer 6

Question 7

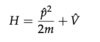
Hamiltonian for Spin-1/2 Particle

Answer 7

• g ≡ g-factor (≈ 2)
• µ_B ≡ Bohr Magneton

Question 8

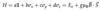
Pauli Matrices

Answer 8

Question 9

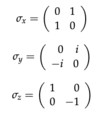
Canonical Quantization

Answer 9

Question 10

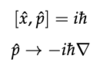
Observable

Answer 10

• For observable A, measurement is eigenstate a_n
  
  • ​wavefunction collapses to eigenstate ψ_n associated with a_n

Question 11

Free Particle in 1D

(Overview)

Answer 11

• Hilbert Space: square-integrable functions on R
• Eigenstates ψ_k of p continuous, but not normalizable
• Eigenenergies Hψ_k = E_kψ_k

Question 12

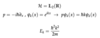
Free Particle in 1D

(Arbitrary State, Orthonormality, Completeness)

Answer 12

Question 13

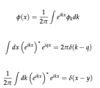
Free Particle in 1D

(Dispersion Relations)

Answer 13

Question 14

Harmonic Oscillator

(Overview)

Answer 14

• Hilbert Space: square-integrable functions in R
• Eigenstates ψ_n and eigenenergies E_n are discrete
• Eigenstates expressed as Hermite polynomials

Question 15

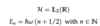
Harmonic Oscillator

(Arbtriary State, Orthonormality, Completeness)

Answer 15

Question 16

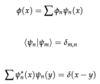
Harmonic Oscillator

(Spectrum and Aribtrary State)

Answer 16

Question 17

Harmonic Oscillator

(Elegant Solution: Overview)

Answer 17

• Introduce lowering and raising operators
• Number operator n = a^†a
• Hamiltonian expressed in number operator
• Vacuum state | 0 > exists with eigenvalue λ = 0
• Arbitrary state formed by applying raising operator to vacuum

Question 18

Harmonic Oscillator

(Elegant Solution: Action of a,a^†)

Answer 18

Question 19

Harmonic Oscillator

(Elegant Solution: Commutation Relations)

Answer 19

Question 20

Harmonic Oscillator

(Elegant Solution: Connection to WF)

Answer 20

Let x = q/a₀

Question 21

Hydrogen Atom

(Overview)

Answer 21

• Consider electron under Born-Oppenheimer approximation in Coulomb potential
• Eigenstates | lmn > of Hamiltonian with eigenenergies E_n
• Can express Hamiltponian in terms of angular momentum L², L_z
  
  • ​Eigenvalues l,m with radial component n

Question 22

Hydrogen Atom

(Orbits)

Answer 22

• E < 0 → closed orbits
• E > 0 → hyperbolic orbits