Chapter 4: Identical Particles

Question 1

Identical Particles

Answer 1

Identical particles are always indistinguishale, because one cannot measure position and momentum simultaneously

• identical ≡ no quantum number or observable to distinguish
• Consider n particles, each with Hilbery Space H₁, basis | α >, and dimension d
  
  • ​Total Hilbert Space H_n
  • Basis | α₁ . . . α_n >
  • Dimension dⁿ

Question 2

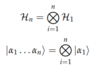
Many-Body Operators

Answer 2

If A is single-particle operator acting on H₁, generalization for n-particles

• A_i acts only on particle i
• All many-body operators are symmetric

Question 3

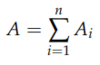
Many-Body Operators

(Momentum)

Answer 3

Question 4

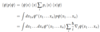
Many-Body Operators

(Density)

Answer 4

Question 5

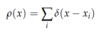
Permutations

Answer 5

• No unique labeling scheme → permutations important
  
  • Permutation are new symmetry, which cannot be broken
• Permutation operator U_Π
  
  • _​unitary
  • operator square-root one → eigenvalues ±1
• Expectation values invariant under permutations → [U_Π, A] = 0
  
  • “identical” ⇐⇒ [U_Π, A] = 0 ∀A which can be measured
• The signum tells you whether you pickup a minus sign when swapping two particles
• Group of all permutations S_n
  
  • ​Two relevant representations: symmetry and anti-symmetric

Question 6

Symmetric Representation

Answer 6

Question 7

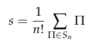
Anti-Symmetric Representation

Answer 7

Question 8

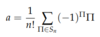
Permutation Hilbert Spaces

Answer 8

• bosons ≡ all symmetric wavefunctions
• fermions ≡ all anti-symmetric wavefunctions

Question 9

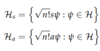
Spin-Statistics Theorem

Answer 9

All (fermions) bosons have (half-)integer spin.

Question 10

Combined Particles

(Two Fermions: Overview)

Answer 10

• Hilbert Space
• Wavefunction →decompose into orbital φ and spin χ part
  
  • NOTE: Either φ or χ can be anti-symmetric, but not both

Question 11

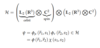
Combined Particles

(Two Fermions: Orbital [Symmetric] Wavefunction)

Answer 11

Question 12

Combined Particles

(Two Fermions: Orbital [Anti-Symmetric] Wavefunction)

Answer 12

Question 13

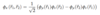
Combined Particles

(Two Fermions: Spin [Symmetric] Wavefunction)

Answer 13

total angular momentum tum s = 1 ≡ triplet state

Question 14

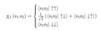
Combined Particles

(Two Fermions: Spin [Anti-Symmetric] Wavefunction)

Answer 14

total angular momentum s = 0 ≡ singlet state

Question 15

Combined Particles

(Two Fermions: Total Wavefunction)

Answer 15

Question 16

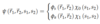
Combined Particles

(Two Bosons)

Answer 16

• Here, no spin
• Higher probability of two bosons being in the same place

Question 17

Combined Particles

(Bose-Einstein Condensate)

Answer 17

Question 18

Ground State of Non-Interacting Fermions

Answer 18

• Eigenstates φ_α(x) with energy E_α
• Project our anti-symmetric part using a
• Resuls in anti-symmetrized Slater determinant

Question 19

Electrons in Free Space

Answer 19

• Electrons form Fermi sea
• NOTE: Place waves cannot be normalized. so introduce elemental volume with PBC
• Density, Fermi energy, and groundstate energy

Question 20

Atoms in Periodic Table

Answer 20

Can undersand via Hydrogen atom up to Argon