Chapter 5: Second Quantization

Question 1

Second Quantization

(Overview)

Answer 1

• Misleading, not quantizing anything, but rather changing representations
• Consider: Many-Body Problem in First Quantization
  
  • Hilbert Space
  • Basis
  • Correct symmetry for particle type

Question 2

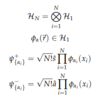
Fock States and Spaces

Answer 2

Question 3

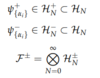
Second Quantization

(Take-Away)

Answer 3

• s,a account for permutations → ordering irrelevant
• Number of modes in {α_i} now important ← new “occupation” representation
• Need to consider what happens with addition/subtraction of mode for both bosons and fermions

Question 4

Second Quantization

(Bosons: Overview)

Answer 4

• Vacuum state ≡ | 0 >
• Creation/annihilation operators a^† , a
• Commutation relations guarantee wavefunction remains symmetric

Question 5

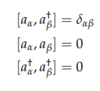
Second Quantizaion

(Bosons: Action of a,a^†)

Answer 5

Question 6

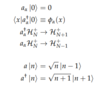
Second Quantization

(Bosons: General State)

Answer 6

State α occupied by N particles

Question 7

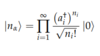
Second Quantization

(Bosons: Notes)

Answer 7

• | { n_α } > form complete basis set for symmetric Fock space
• Order unimportant for bosons
  
  • Creation/annihilation operators act only on specific state
• Total number operator N_tot

Question 8

Second Quantization

(Bosons: Connection to Wavefunction)

Answer 8

Question 9

Second Quantization

(Fermions: Overview)

Answer 9

NOTE: Similar to bosons with + → − and a few exceptions

• Commutator not well defined
• Operators anti-commute

Question 10

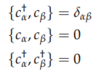
Second Quantization

(Fermions: Actions of c, c^†)

Answer 10

Question 11

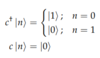
Second Quantization

(Fermions: General State)

Answer 11

Question 12

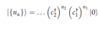
Second Quantization

(Fermions: Notes)

Answer 12

Ordering is important

Question 13

Second Quantization

(Single-Particle Operator)

Answer 13

Let A_i be single-particle operator

Question 14

Second Quantization

(Two-Particle Operator)

Answer 14

Let A_ij be a two-particle operator

Question 15

Second Quantization

(Basis Transformation)

Answer 15

• Let φ_α(x), χ_ν(x) be complete, orthonormal basis sets with (creation) annihilation operators a_α^(†) , b_ν^(†)
  
  • ^​NOTE: Commutation relation still holds

Question 16

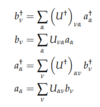
Field Operator

(Overview)

Answer 16

• Recall: single-particle wavefunction φ_αs(r) in mode α with spin s
• Field operator creates/destroy particle at r

Question 17

Field Operator

(Commutation Relations)

Answer 17

(Anti-)Commutators follow as that for (fermions) bosons

• Bosons
• Fermions

Question 18

Field Operator

(General State)

Answer 18

Question 19

Field Operator

(Take-Away)

Answer 19

• Can always swtich between these two:
  
  • wavefunction picture ⇐⇒ first quantization
  • state picture ⇐⇒ second quantization

Question 20

Field Operator

(Single-Particle Operator)

Answer 20

Let A₁ be single-particle operator

Question 21

Field Operator

(Two-Particle Operator)

Answer 21

Let A₂ be two particle operator

• NOTE: ψ^†(r₁)ψ^†(r₂)ψ(r₂)ψ(r₁) ordering removes self-interaction

Question 22

Field Operator

(Hamiltonian)

Answer 22

Question 23

Correlations in Non-Interacting Fermi Gas

(Green’s Function)

Answer 23

NOTE: j₁ is Bessel function

Question 24

Correlations in Non-Interacting Fermi Gas

(Green’s Function: Graph)

Answer 24

Question 25

Correlations in Non-Interacting Fermi Gas

(Pair Correlation Function)

Answer 25

Question 26

Correlations in Non-Interacting Fermi Gas

(Pair Correlation Function: Graph)

Answer 26

Question 27

Quantization of Electric Field

Answer 27

• Until now, went from single-particle quantization → second quantization
• Can also quantize electromagnetic field directly
  
  • Decomposes into uncoupled harmonic oscillators

Question 28

Quantization of Electric Field
(Creation/Annihilation Operators, Commutator.
Hamiltonian, Arbitrary State)

Answer 28

• a^†_<em>kλ</em> produces photon in mode k, λ

Question 29

Quantization of Electric Field

(Vector Potential in Heisenberg Picture)

Answer 29

Question 30

Quantization of Electric Field

(Canonical Commutation Relations)

Answer 30

NOTE: Only valud for equal time

Question 31

Quantization of Electric Field

(Canonical Commutation Relations: Graph)

Answer 31

Only non-zero in shaded region

Question 32

Photon Characteristics

(Energy)

Answer 32

Question 33

Photon Characteristics

(Momentum)

Answer 33

Question 34

Photon Characteristics

(Spin)

Answer 34

• Spin is ±(hbar) along k
• For massless particles at speed of light, spin is always along axis of propagation with values ±1

Question 35

Photon Characeristics

(Angular Momentum)

Answer 35

NOTE: Choosing circularly polarized light basis results in well-defined spin

Question 36

Quantization of Electric Field

(Notes)

Answer 36

• For single photon, expectation value of electric field vanishes
  
  • Also for state with fixed number of photons
• Fluctuations of field in vacuum at same position are infinite
  
  • Not a problem, because any detector measures over finite area/volume