Chapter 3: Perturbation Theory Flashcards
(13 cards)
Pertubation Theory
(Overview)
a systematic procedure forobtaining approximate solutions to the perturbed problem by building on the known exact solutions o the unperturbed state
- Exact Hamiltonian H0 is perturbed by small correction H`
- Total Hamiltonian H expanded in series of λ << 1
- Here, consider only time-independent, discrene energy spectra {En}
- Often good enregies, but poor wavefunctions

Non-Degenerate Case
(Assumptions)
- Time-independent
- {En} are pair-wise different
Non-Degenerate Case
(Energy Correction: First-Order)
expectation value of the perturbed Hamiltonian in the unperturbed state

Non-Degenerate Case
(Energy Correction: Second-Order)
- Always* reduces the ground-state energy
- E2n* <= 0
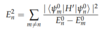
Non-Degenerate Case
(Energy Correction: General)
For corrections k = 1, 2, 3, …

Non-Degenerate Case
(State Correction: First-Order)
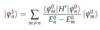
Non-Degenerate Case
(State Correction: General)
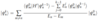
Degenerate Case
(Assumptions)
- These exists degeneracy in energies
- Goal: Diagonalize the perturbed Hamiltonian H’ in basis of degenerate states
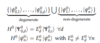
Degenerate Case
(Energy Correct: First-Order [Two-Fold Degeneracy])
Theorem Let A be Hermitian operator with [A.H**‘] = 0. If states |a> and |b> are eigenstates of A with distinct values, then Wab = 0
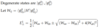
Degenerate Case
(Energy Correct: First-Order [General])
Diagonalize perturbed Hamiltonian H’ in basis of degenerate states
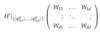
Degenerate Case
(State Correction: First-Order [Two-Fold Degeneracy])
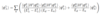
Degenerate Case
(State Correction: General)
- There exists recursive formula for state correction with arbitrary degeneracy
Degenerate Case
(Higher Order Corrections)
- If first-order correction lifts degeneracy, use non-degenerate perturbation theory
- If degeneracy remains, need to diagonalize perturbation in second- or higher order


