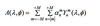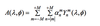Chapter 5: spectral models Flashcards
Spectral models are also based on
the Primitive Equations.
Spectral models are also based on the Primitive Equations.
But their
mathematical formulation and numerical solutions are quite different from Grid Point Models for some of the forecast variables
Spectral Models were developed as a means of
increasing the speed while enhancing the resolution for global forecasting.
spectral Models were developed as a means of increasing the speed while enhancing the resolution for global forecasting.
However, as the resolution of the grid point formulations is also increasing day- by-day with the advent of
powerful computers
However, as the resolution of the grid point formulations is also increasing day- by-day with the advent of powerful computers, the use of spectral methods may lessen due to
their complex mathematics
However, as the resolution of the grid point formulations is also increasing day- by-day with the advent of powerful computers, the use of spectral methods may lessen due to their complex mathematics and more global models may begin using
grid point formulations.
Spectral Models use
a combination of continuous waves of differing wavelengths and amplitudes
Spectral Models use a combination of continuous waves of differing wavelengths and amplitudes to
specify the forecast variables and their derivates at all locations.
Instead of using …………………., Spectral Models use a combination of continuous waves of differing wavelengths and amplitudes to specify the forecast variables and their derivates at all locations.
grid points
Conceptually, Spectral Models follow the process of
drawing contours through a data field to represent the forecast variables.
Since spectral models represent
some of the FV’s with continuous waves rather than at separate points along a wave
since spectral models represent some of the FV’s with continuous waves rather than at separate points along a wave, they can use
more accurate numerical techniques to solve some of the equations on much longer forecast time steps than the finite difference methods used by grid point models.
Since spectral models represent some of the FV’s with continuous waves rather than at separate points along a wave, they can use more accurate numerical techniques to solve some of the equations on much longer forecast time steps than the finite difference methods used by grid point models.
However, some grid point calculations are
required (for model physics) in spectral models
However, some grid point calculations are required (for model physics) in spectral models and this introduces
some computational errors associated with grid point models.
However, some grid point calculations are required (for model physics) in spectral models and this introduces some computational errors associated with grid point models.
Thus the more ………………………….. the …………………………………..
the more physics that is involved in the evolution of the forecast, the less the advantage in spectral model forecasts compared to comparable resolution grid point forecasts.
Spectral methods are most commonly used for
global numerical weather prediction
Spectral methods are most commonly used for global numerical weather prediction, with the primitive equations solved in
spherical rather than Cartesian coordinates, at operational forecast centers.
examples of spectral models
the NCEP Global Forecast System and the
ECMWF Integrated Forecast System models
global models need not be
spectral models
However, global models need not be spectral models, nor is the use of spectral models limited to
global applications.
basis functions
Spectral modeling for NWP is based on the Galerkin Method, in which the dependent variables are approximated by a finite sum of linearly independent functions
The general form of approximating some function f(x) by a finite sum of basis functions is given by:
The general form of approximating some function f(x) by a finite sum of basis functions is given by
For example, if the function f is a function of
both time t and space x, the above equation takes the form:
in this equation
the spatial variability is captured by the basis functions, while temporal variability is captured by the coefficients of the base functions.
In spectral models, the basis functions are referred to as
spherical harmonics
in spectral models, the basis functions are referred to as spherical harmonics.
• In these models, the basis functions take the form of
Fourier series
legendre function
In these models, the basis functions take the form of Fourier series, where
zonal variability in the dependent variables is represented by series of sine and cosine waves of varying wavelength,
Legendre functions
depict meridional variability in the dependent variables.
in spectral models, the basis functions are referred to as spherical harmonics.
- In these models, the basis functions take the form of Fourier series, where zonal variability in the dependent variables is represented by series of sine and cosine waves of varying wavelength, and
- Legendre functions, which depict meridional variability in the dependent variables. These basis functions are
continuous across the sphere
Fourier series, with sines and cosines serving as the basis functions, are used to represent
zonal variability in the dependent variables
For a generic function A(x) its Fourier series expansion is given by:
Legendre functions serve as the basis functions to represent
meridional variability in the dependent variables.
for a generic function A(lamda, o|) where lamda is …….. and o| is …………….. its spherical expansion is given by:
lamda is longitude
o| is latitude
what does the following represent
m
M
n
N
m is the zonal wavenumber (no. of waves on a circle of latitude)
M is the highest-permitted zonal wavenumber
n (a positive integer) is the order of the associated Legendre function,
N is the highest-permitted order of the associated Legendre function,
what does the following represent
amn
Ymn
spectral coefficients
spherical harmonics
For example, the zonal variation of a meteorological variable, say T(x) can be represented in terms of a zonal mean plus a finite Fourier series as :
where Ti is
temperature at ith point on the latitude circle
If we assume that 3 points are sufficient to capture the information contained in each of a series of continuous waves, i varies as 1,2,3,……,m (=3n)
For example, the zonal variation of a meteorological variable, say T(x) can be represented in terms of a zonal mean plus a finite Fourier series as :
where n is
Total number of waves used to describe the temperature field
In spectral models, the horizontal resolution is designated by a T number (e.g., T80), which indicates the number of waves used to represent the data
For example, the zonal variation of a meteorological variable, say T(x) can be represented in terms of a zonal mean plus a finite Fourier series as :
where k is
Zonal wave number – the number of waves along a latitude circle For example, k=10 implies a wavelength of L=360o/10=36o.
For example, the zonal variation of a meteorological variable, say T(x) can be represented in terms of a zonal mean plus a finite Fourier series as :
where A0 is
Zonal mean, which is considered to be wave number zero.
For example, the zonal variation of a meteorological variable, say T(x) can be represented in terms of a zonal mean plus a finite Fourier series as :
where Ak and Bk
Coefficients which are obtained using the discrete Fourier transforms
For example, the zonal variation of a meteorological variable, say T(x) can be represented in terms of a zonal mean plus a finite Fourier series as :
…………………. can be used to obtain Ak and Bk
The observed temperature data
In spectral models, the horizontal resolution is designated by
a “T” number (for example, T80)
In spectral models, the horizontal resolution is designated by a “T” number (for example, T80), which indicates the
Number of waves used to represent the data.
In spectral models, the horizontal resolution is designated by a “T” number (for example, T80), which indicates the number of waves used to represent the data. The “T” stands for
triangular truncation
The “T” stands for triangular truncation, which indicates
the particular set of waves used by a spectral model.
Spectral models represent data precisely
out to a maximum number of waves, but omit all, more detailed information contained in smaller waves.
Spectral models represent data precisely out to a maximum number of waves, but omit all, more detailed information contained in smaller waves.
This accurate representation up to
a cut-off and then complete omission is in contrast to grid point models,
This accurate representation up to a cut-off and then complete omission is in contrast to grid point models, which try to represent
all scales but poorly handle waves only a few grid points across.
The wavelength of the smallest wave in a spectral model is represented as:
minimum wavelength = 360o/N where N is the total no. of waves (T number)
We can approximate the grid spacing to obtain
equivalent accuracy to a spectral model with a fixed number of waves using a very simple approach.
We can approximate the grid spacing to obtain equivalent accuracy to a spectral model with a fixed number of waves using a very simple approach
In fact, the dynamics of spectral models retain far better
wave representation than grid point models with this grid spacing.
In fact, the dynamics of spectral models retain far better wave representation than grid point models with this grid spacing.
However, the spectral model physics is calculated on
a grid, with about three times as many grid lengths as number of waves used to represent the data
However, the spectral model physics is calculated on a grid, with about three times as many grid lengths as number of waves used to represent the data.
since it takes …………………. to represent
five to seven grid points to represent ‘wavy’ data well and even more for features that include discontinuities
Since it takes five to seven grid points to represent ‘wavy’ data well and even more for features that include discontinuities, the resolution of the physics is
poorer than the above formulation indicates and degrades the quality of the spectral model forecast.
In triangular truncation,
the highest degree of the various spherical harmonics Ymn (m denotes the zonal wave number and n the order) is fixed and is set equal to the highest order of these a waves.
in triangular trunctation the highest degree of the various spherical harmonics Ymn (m denotes the zonal wave number and n the order) is fixed and is set equal to the highest order of the sea waves.
under this truncation, ….
different wavenumbers m have different degrees of freedom along a latitude.
Having the advantages of better resolution, attempts have been made to apply
the spectral method to a limited area also.
Sine functions which form a basis of
orthogonal functions on [0,2pi] can however be used for expanding only periodic functions over the plane domain under consideration.
Sine functions which form a basis of orthogonal functions on 0,2 can however be used for expanding only periodic functions over the plane domain under consideration.
One of the techniques proposed for using a basis of sine functions effectively is to
use doubly period fields in spectral LAMs.
One of the techniques proposed for using a basis of sine functions effectively is to use doubly period fields in spectral LAMs.
In this technique, the working domain is
enlarged
In this technique, the working domain is enlarged (Figure) so as to
extend the fields so that they, and their space derivatives, are periodic in both directions over the new domain
so as to extend the fields so that they, and their space derivatives, are periodic in both directions over the new domain; the spectral method can then be applied to
these doubly periodic fields.
The procedure consisting in extending the
domain and constructing doubly periodic fields on the domain R provides a simple way of using the spectral method on a limited domain.
The procedure consisting in extending the domain and constructing doubly periodic fields on the domain R provides a simple way of using the spectral method on a limited domain.
This allows
the space derivative to be calculated very accurately
The development of operational weather forecasting models requires
a very big investment.
The development of operational weather forecasting models requires a very big investment. We can consider using
a single basis code to obtain both a spherical model and a limited area model.
