ch2: Finite Differences Flashcards
A Taylor series is
express the first derivative of the following is
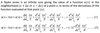
Taylor’s series expansion can be used to
express the derivatives
The expressions on the RHS of (3) and (4) that are used to express
the space derivatives, are called the forward and backward finite differences.
The difference between the derivative and its finite difference expression is shown in the following diagram.
what is the tangent and secant line
The straight line that”just touches” the curve at a point is the tangent, while the line that intersects two points on the curve, is the secant line.
what does the tangent and secant line represent
the slope of atangent line represents the derivative, the slope of a secant line represents the finite difference.
as /-\x approaches zero
the slope of the secant line approaches the slope of the tangent line. Then, the finite difference will be the true derivative.
The fundamental equations governing the atmospheric motion consist of
non‐ linear partial differential equations, which do not have analytical solutions and are solved using numerical methods.
The fundamental equations governing the atmospheric motion consist of non‐ linear partial differential equations, which do not have analytical solutions and are solved using numerical methods.
These equations include
spatial derivatives at a fixed point, which can be approximated based on Taylor’s expansion of the variable about that point
from the taylor’s series expansion (1 & 2), ………………………….. may be formulated for the ………………………………………………..
three different expressions
approximation of the first derivative of the function u at x
The forward and backward difference expressions can be obtained from (1) & (2):
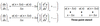
The centered difference expression can be obtained by
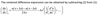
Thus the error (truncation error)
Thus, the first derivative can be approximated by forward, backward and center
difference formulae as:
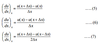
The second order ……………….. accurate second derivative of ………. may be easily obtained by
The Laplacian operator
The Laplacian operator appears in many diagnostic and prognostic equations in meteorology. The application of its finite analog is found to be very practical for the solution of many problems.
The Laplace’s equation takes the form:
The 3D and 2D Laplacian operator in Cartesian coordinate system, can be expressed as:
let ………………. be any scalar function of …………………………… the finite difference analog of ………………………………………….. will be evaluated with reference to ……………………. as follows
use taylor series to expand a function of two variables
there is ……………………………… which also gives second order accurate results this uses …………………………………….
using …………………………. is slightly more accurate than ………………………………………….
Using a 5‐point diamond stencil is slightly more accurate than a 5‐point square stencil
Using a 5‐point diamond stencil is slightly more accurate than a 5‐point square
stencil. this is because
the distance from the center point (I,J) to the other points is less in the diamond stencil than the corresponding distance in the square stencil.
Jacobian is also
a common operator encountered during the solution of many geophysical problems. It appears mostly in the non‐linear advective terms.
Jacobian is also a common operator encountered during the solution of many geophysical problems. It appears mostly in the non‐linear advective terms.
For example
