ch3: Barotropic model Flashcards
(14 cards)
In Barotropic model atmosphere, some of the following conditions exist throughout the motion:
- coincidence of pressure and temperature surfaces;
- absence of vertical wind shear;
- absence of vertical motions;
- absence of horizontal velocity divergence; and
- conservation of the vertical component of absolute vorticity
Barotropic models are usually divided into two classes:
- the nondivergent barotropic model and
- the divergent barotropic model (also called the shallow‐water equations).
The simple nondivergent barotropic model is based on
the barotropic vorticity equation.
The Barotropic (Nondivergent ) Model
- This model is based on an assumption that the absolute vorticity is conserved, which applies to a barotropic atmosphere or at the level of non divergence.
- The barotropic models have shown their usefulness for tropical wind prediction especially at those levels where the divergence is small.
The barotropic vorticity equation describes
the evolution of a homogeneous (constant density), non‐divergent, incompressible flow, in which the absolute vorticity is conserved following the motion:

The barotropic model is obtained from
the barotropic vorticity equation
the barotropic vorticity equation

the jacobian can be defined in three equivalent ways
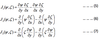
It turns out that none of the above finite difference analogs for the Jacobian conserves

both kinetic energy and mean square vorticity over the model domain.
They are, therefore, not suitable for use in the model
t turns out that none of the above finite difference analogs for the Jacobian conserves both kinetic energy and mean square vorticity over the model domain.
They are, therefore, not suitable for use in the model
However, Arakawa has shown that
the linear combination as shown below conserves them.
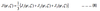
Let us write expressions for J1, J2 and J3 using a 9‐point stencil as shown in Fig.

Time Derivatives
- The Leap‐frog time differencing scheme can be used in this model.
- that is, a forward difference for the first time step and then a central difference for the next time steps:
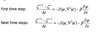
Implementation of the Model
Assumptions and Simplification


