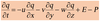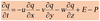ch1: Dynamic Review Flashcards
Certain physical laws of motion and conservation of energy govern
the evolution of the atmosphere.
………………………………………… govern the evolution of the atmosphere
Certain physical laws of motion and conservation of energy
Certain physical laws of motion and conservation of energy govern the evolution of the atmosphere.
These laws can be converted into a series of ……………………….. that
mathematical equations
make up the core of what we call numerical weather prediction
……………………………………… that make up the core of what we call numerical weather prediction
Certain physical laws of motion and conservation of energy govern the evolution of the atmosphere.
These laws can be converted into a series of mathematical equations
If we know the initial conditions of the atmosphere, we can solve
these equations to obtain new values of those variables at a later time (i.e., make a forecast)
…………………………………………..we can solve these equations to obtain new values of those variables at a later time (i.e., make a forecast)
If we know the initial conditions of the atmosphere
An NWP model can be represented mathematically, in its simplest form as:
The above equation can be expressed in words as
‘the change in forecast variable A during the time period is equal to the cumulative effects of all processes (physical forcings) that force A to change’
In NWP, future values of meteorological variables are solved by
finding their initial values and then adding thephysical forcingthat acts on the variables over the time period of the forecast.
F(A) stands for the combination of all of the kinds of forcing that can occure
Example: Suppose today’s temperature is 32oC and the temperature is found to increase at a rate of 0.2oC/6 hrs. Find tomorrow’s temperature.
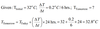
The equations used to build the various types of models for simulating the evolution of the atmosphere are obtained from
the basic general equations by making a number of simplifications.
……………………………. are obtained from the basic general equations by making a number of simplifications.
The equations used to build the various types of models for simulating the evolution of the atmosphere
The equations used to build the various types of models for simulating the evolution of the atmosphere are obtained from the basic general equations by making a number of simplifications.
These simplifications are justified by:
- analysis of the order of magnitude of the various terms in the equations for the scales to be representedand
- the degree of simplification to be achieved so as to simulate the behavior of the atmosphere
Atmospheric models are built from:
- the momentum equations (equations of motion)
- the mass conservation equation (orcontinuity equation)
- the energy conservation equation (or thethermodynamic equation)
- the water vapor conservation equation, and
- the equation of state
The momentum equations, derived from
the Newton’s second law
The momentum equations, derived from the Newton’s second law, allow us to calculate
the acceleration of air parcelsin terms of the forces (PGF, Coriolis Force, Gravity and Friction) acting up on them
……………………………………… allow us to calculate theacceleration of air parcelsin terms of the forces (PGF, Coriolis Force, Gravity and Friction) acting up on them.
The momentum equations, derived from the Newton’s second law
These equations for the motion of a unit mass of air (parcel of air) in a frameof
reference attached to the Earth and having its origin located at the Earth’s center
(spherical coordinates), can be expressed as:
………………………………………………… can be expressed at
These equations for the motion of a unit mass of air (parcel of air) in a frameof reference attached to the Earth and having its origin located at the Earth’s center (spherical coordinates)
the term proportional to …………………………………… account for …………………………………..
1/a (whereais distance from the center of the Earth) account for the spherical geometry of the Earth.
By calculating all the relevant forces acting on the parcels of air, we can calculate
any changes to the speed of movement of air parcels – essentially allowing us to forecast the wind speed.
…………………………………….. essentially allowing us to forecast the wind speed.
By calculating all the relevant forces acting on the parcels of air, we can calculate any changes to the speed of movement of air parcels
Conservation of Mass (continuity equation)
Following a parcel of air along its trajectory, the mass of that parcel, M, cannot be
changed, although its shape and volume may vary.
Expressing this in terms of the parcel’s density (p) and volume (divergence or convergence) gives the
continuity equation
……………………………………………………..
Following a parcel of air along its trajectory, the mass of that parcel,M, cannot be changed, although its shape and volume may vary.
convertion of mass (continuity equation)
……………………………………………………………… gives ……………………………
Expressing this in terms of the parcel’s density (p) and volume (divergence or convergence) gives the continuity equation
The thermodynamic equation, derived from
the principle of conservation of energy, gives the temperature changes at a fixed point (local rate of change or Eulerian rate) in space as
………………………………………………… derived from the principle of conservation of
energy, gives the temperature changes at a fixed point (local rate of change or
Eulerian rate) in space as
thermodynamic equation
Conservation of water is usually expressed in terms of
mixing ratio, q (i.e., mass of water vapor per unit mass of dry air)
Changes in water vapor at a fixed point due to advection of water vapor by the
wind field together with sources and sinkscan be expressed as:
Changes in water vapor at a fixed point due to advection of water vapor by the
wind field together with sources and sinks
……………………………. is usually expressed in terms ofmixing ratio, q (i.e., mass of water vapor per unit mass of dry air).
conservation of water
The Equation of State
This is a diagnostic relationship between the fundamental thermodynamic variables (pressure, temperature and density etc.)
Knowing any two thermodynamic quantities of a parcel, the equation of state allows the
calculation of any other thermodynamic variable
In meteorology the usual form of the equation of state is:
………………………………….
This is a diagnostic relationship between the fundamental thermodynamic
variables (pressure, temperature and density etc.)
the equation of state
………………………………………………. allows the calculation of any other thermodynamic variable
Knowing any two thermodynamic quantities of a parcel, the equation of state
In meteorology the usual form of the equation of state is
in the equations F, Q and M represents
the friction, Q and M (=E-P) represent the source and sink terms for heat and specific humidity, respectively.
These physical terms are expressed in terms of the forecast variables, by a process called
parameterization
The above set of general or basic hydrodynamical equations (1‐7) represent
all scales of atmospheric motions.
These basic hydrodynamical equationsare simplified by
applying approximations or assumptions that are applicable to a particular scale of motion to obtain different types of model equations.
For an adiabatic friction less and water vapor conserving atmosphere, the physical terms (F,Q and M) are equal to
zero
……………………. represents the friction, Q and M (=E-P) represent the source and sink terms for heat and specific humidity, respectively.
F
by a process called parameterization
These physical terms are expressed in terms of the forecast variables
…………………………………………. represent all scales of atmospheric motions
The above set of general or basic hydrodynamical equations (1‐7)
………………………………. to obtain different types ofmodel equations
These basic hydrodynamical equations are simplified by applying approximations or assumptions that are applicable toa particular scale of motion
…………………………………….. are equal to zero
For an adiabatic frictionless and water vapor conserving atmosphere,the physical
terms (F,Q and M)
In general, approximations are applied to
the basic hydrodynamical equations
In general, approximations are applied to the basic hydrodynamical equations to:
- simplify the solutions of the equations and save the computing time or
- to filter out undesirable, non‐meteorological solutions of the equations
With increasing computing power together with advances in the mathematical methods used to solve the equations, modern NWP systems tend to
make fewer approximations to the equations.
………………………………………….. tend to make fewer approximations to the equations.
With increasing computing power together with advances in the mathematical methods used to solve the equations, modern NWP systems
The traditional approximation in meteorology consists in
approximating the atmosphere to a thin layer
The traditional approximation in meteorology consists in approximating the atmosphere to athin layerand leads to
a system of nonhydrostatic equations that allows for the proper handling of mesoscale atmospheric motionin particular.
When the atmosphere is considered as a thin layer, several simplifications can be made through
scale analysis of the various terms in the equations
When the atmosphere is considered as a thin layer, several simplifications can be
made through scale analysis of the various terms in the equations.:
- First, the ellipticity of the terrestrial geoid is ignored and acceleration due to gravity g is assumed constant.
- Second, the radial distanceris replaced by the mean radius aof an assumed spherical Earth (thin layer approximation).
- The coriolis terms in cos y which are smaller compared to the other terms are neglected.
- Several metric terms (the components of the derivatives of the unit vectors) are also ignored.
By applying the above simplifications, we obtain
the system of nonhydrostatic equationsfor an adiabatic frictionless atmosphere.
……………………………………………………………………………that allows for the proper handling of mesoscale atmospheric motionin particular.
The traditional approximation in meteorology consists in approximating the
atmosphere to athin layerand leads to a system of nonhydrostatic equations
………………………………………………………………. several simplifications can be made through scale analysis of the various terms in the equations
When the atmosphere is considered as a thin layer
Simplification of horizontal momentum equations (1 and 2)
Simplification of vertical momentum equation (3)
Thermodynamic energy equation (5)
Continuity and Thermodynamic equations (4 & 5) are combined
These five equations (8‐12) describe
the evolution of five meteorological variables: the three components of wind velocity, plus temperature and pressure.
Thesefiveequations(8‐12) describe the evolution of five meteorological
variables: the three components of wind velocity, plus temperature and pressure.
This system of equations can be used to
- model atmospheric flows over a wide spectrum of spatial scales, from theplanetary scale to the mesoscale.
- It allows us to simulate the propagation of Rossby waves, inertia‐gravity waves,andeven sound waves.
This system of equations can be used to model atmospheric flows over a wide spectrum of spatial scales, from theplanetary scale to the mesoscale. It allows us to simulate the propagation of Rossby waves, inertia‐gravity waves,andeven sound waves.
because of ……………………………….. it cannot be used to ………………………………
Because of the thin layer approximation, it cannot be used to simulate geophysical fluids with large vertical extension (e.g. the gaseous planets).
If we are interested in the synoptic scalesfor which the vertical velocities are an order of magnitude smaller than the horizontal velocities, we can
ignore the vertical acceleration dw/dt in the vertical velocity equation.
if we are intereseted in ………………………………………………………………………. we can ignore the vertical acceleration dw/dt in the vertical velocity equation.
the synoptic scalesfor which the vertical velocities are an order of magnitude smaller than the horizontal velocities
The vertical velocity equation (10) then becomes
a diagnostic relation (i.e. where the variable t does not appear) known as thehydrostatic balance equation
…………………………………………… known as thehydrostatic balance equation
The vertical velocity equation (10) then becomes a diagnostic relation (i.e. where
the variable t does not appear)
The hydrostatic assumption is justified for
the terrestrial atmosphere if we are to look at phenomena whose horizontal scale exceeds 10 km or so.
……………………….is justified for the terrestrial atmosphere if we are to look at phenomena whose horizontal scale exceeds 10 km or so.
The hydrostatic assumption
When the above hydrostatic equation is added to
the other four equations (8, 9, 11 & 12), gives the system of fiveprimitive equationsfor an adiabatic frictionless atmosphere.
the following are
The system of primitive equations for an adiabatic frictionless atmosphere
This system of equations is relevant for
simulating atmospheric motion whose horizontal space scale is greater than about 10 km, which excludes its use for the explicit modelling ofconvection.
This system of equations is relevant for simulating atmospheric motion whose horizontal space scale is greater than about 10 km, which excludes its use for the explicit modelling ofconvection.
It allows us to take into account
Rossby waves and inertia gravity waves
This system of equations is relevant for simulating atmospheric motion whose horizontal space scale is greater than about 10 km, which excludes its use for the explicit modelling ofconvection.
It allows us to take into account Rossby waves and inertia gravity waves; but nevertheless,it
eliminates sound waves because of the hydrostatic relation which has a filtering effect on them.
Theprimitive equationsare the basis of
most NWP models.
Anelastic Approximation
This approximation involves
neglecting the time derivative of density in the continuity equation
the anelastic approximation
This effectively states that
three‐dimensional divergence of air must be zero, or that horizontal divergence must be balanced by vertical acceleration which acts to maintain the air density.
This effectively states that three‐dimensional divergence of air must be zero, or that horizontal divergence must be balanced by vertical acceleration which acts to maintain the air density.
This approximation also
filters out horizontally propagating sound waves as a solution to the equation set, since these waves require three‐dimensional divergence in order to propagate
In the quasi‐geostrophic approximation, winds are
approximated by their geostrophic (i.e. exactly proportional to the pressure gradient)
In the quasi‐geostrophic approximation, winds are approximated by their geostrophic (i.e. exactly proportional to the pressure gradient) values in
- the acceleration terms in the momentum equation and
- the advection terms in the temperature equation.
In the quasi‐geostrophic approximation, winds are approximated by their
geostrophic (i.e. exactly proportional to the pressure gradient) values in
• the acceleration terms in the momentum equation and
• the advection terms in the temperature equation.
In this system of equations, …………………………. negelcted ………………….
vertical acceleration is also neglected (i.e. the hydrostatic approximation is made).
The quasi‐geostrophic equations filter out
sound waves, gravity waves and inertial oscillations.
The quasi‐geostrophic equations filter out sound waves, gravity waves and
inertial oscillations.
However, the system had …………………………. for ………………………………………. since it
limited application for weather forecasting, since it could not describe small scale motions of importance to weather forecasting, such as mesoscale circulations in frontal zones.
Therefore, as stated earlier, with increasing computing power together with advances in the mathematical methods, the present NWP models are based on
the more accurate primitive equations rather than the highly approximated quasi‐geostrophic system
