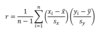chapter 4: scatterplots and correlation

Question 1

The plan phase of a two-variable scatterplot scenario might be phrased like this:

Answer 1

Make a scatterplot with “[variable 1]” as the explanatory variable and “[variable 2]” as the response variable. Describe the form, direction, and strength of the relationship.

Question 2

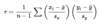
To add a categorical variable to a scatterplot:

Answer 2

use a different plot color or symbol for each category.

Question 3

True or false: Our eyes can be fooled by changing the plotting scales or the amount of space around the cloud of points in a scatterplot

Answer 3

true

Question 4

correlation

Answer 4

measures the direction and strength of the linear relationship between two quantitative variables. Correlation is usually written as r.

Question 5

True or false: Correlation makes no distinction between explanatory and response variables.

Answer 5

True

Question 6

Evaluating r.

Answer 6

The correlation r is always a number between −1 and 1. Values of r near0 indicate a very weak linear relationship. The strength of the linearrelationship increases as r moves away from 0 toward either −1 or 1.Values of r close to −1 or 1 indicate that the points in a scatterplot lie close to a straight line.

Question 7

When examining a relationship between two quantitative variables, we look at:

Answer 7

form, direction, strength, and outliers.

Question 8

univariate data

Answer 8

data that includes a single variable

Question 9

multivariate data

Answer 9

data that includes two or more variables

Question 10

bivariate data

Answer 10

data that has only two variables

Question 11

You describe a scatterplot with these criteria

Answer 11

direction, form (curved, straight, oscillating) and strength (scatter from the mean)

Question 12

𝑠_x

Answer 12

standard deviation of an individual

Question 13

r

Answer 13

correlation

ranges between -1 and +1

-1 ≤ r ≤ 1

closer to ones is stronger +/- association

only makes sense with linear data