chapter 2: describing distributions with numbers

Question 1

measures

Answer 1

results of functions applied to the data

Question 2

n

Answer 2

the number of observations in our dataset

Question 3

mode

Answer 3

value that appears most often

Question 4

we call the dataset “bimodal” or “multimodal” when…

Answer 4

when many values appear the same number of times, and sometimes there will be two or more modes

Question 5

𝑥_𝑖

Answer 5

the value of the 𝑖^th observation in an ordered dataset

Question 6

The median M

Answer 6

the observation that has just as many observations to the left of it as to the right of it, or the value in our dataset that is greater than just as many values in our dataset as it is less than. To find its location (not its value) you use (n+1)/2.

Question 7

The minimum (or min) and maximum (or max)

Answer 7

the first and last in the list–or the smallest and the greatest values in our dataset - respectively

Question 8

range

Answer 8

The difference between the max and the min

Question 9

The first and third quartiles, (𝑄₁ and 𝑄₃)

Answer 9

the median of the values less than the median and the median of the values greater than the median, respectively. You calculate quartiles the way you calculate the median M

Question 10

five-number summary

Answer 10

a listing of these five values: minimum, Q₁, median, Q₃, and maximum)

Question 11

box plot

Answer 11

A visual representation of the five-number summary

Question 12

inter-quartile range (IQR)

Answer 12

the difference between the third and first quartiles,

or

IQR = 𝑄₃ − 𝑄₁

Question 13

Outlier Rule

Answer 13

If an observation has a value greater than 𝑄3 + (1.5 × 𝐼𝑄𝑅) or less than 𝑄1– (1.5 × 𝐼𝑄𝑅), then it can be considered an outlier

Question 14

The five-number summary is ideal for [blank]

Answer 14

skewed data or data with outliers

Question 15

True or false: Boxplots of multiple populations can be graphs together to compare their means and spreads

Answer 15

True

Question 16

mean

Answer 16

an alternate measure of center, and will have the same units as our observations. Notice that when a median or quartile falls between two observations, we use the mean of their values

Question 17

the mean x̄ formula

Answer 17

x with a line over it (the mean) = 1 divided by n (the number of observations) times—i.e. the following divided by n— capital Sigma (the sum of) x(dropped I) (each observation in the ordered) dataset. In other words, the average of the observations.

Question 18

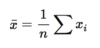
standard deviation s

Answer 18

an alternate measure of variability, and will also have the same units as the observations. Standard deviation is an “average” of how far observation values are from the mean of the dataset. It is the square root of the variance s²

Question 19

the variance of the dataset s²

Answer 19

The variance s^₂ of a set of observations is an average of the squares of the deviations of the observations from their mean.

Question 20

the formula for standard deviation

Answer 20

the square root of: 1 divided by n(number of observations) minus 1times—i.e. the following divided by n-1)—Sigma(the sum of) x(dropped i) (each observation) minus the mean, squared

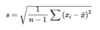
Question 21

s

Answer 21

The standard deviation. This measures variability about the mean and should be used only when the mean is chosen as the measure of center. s is always zero or greater than zero. s = 0 only when there is no variability. s has the same units of measurement as the original observations.

Question 22

resistant measures

Answer 22

depend only upon the ordering of the data

Question 23

non-resistant measures

Answer 23

depend on the particular values of the observations (mean, standard deviation, and variance)

Question 24

the mean and the median will coincide if…

Answer 24

our distribution is symmetric

Question 25

the mean will be further out in the tail if…

Answer 25

our distribution is skewed

Question 26

proportions for our dataset

Answer 26

e.g. the number of observations witha value less than a given value over the size of the dataset

Question 27

Σ

Answer 27

(capital sigma) means add them all up

Question 28

x̄

Answer 28

the mean, or numeric average of the observations, add the values and divide by number of observations

Question 29

True or false: the mean x̄ is resistant to outliers

Answer 29

True. Because the mean cannot resist the influence of extreme observations, we say that it is not a resistant measure of center.

Question 30

n - 1

Answer 30

The degrees of freedom of the variance or standard deviation. When finding the variance, we divide the sum by one fewer than the number of observations. The reason is that the deviations x_i - x̄ always sum to exactly 0 so that knowing n − 1 of them determines the last one.

Question 31

choosing a summary (the five number summary vs. x̄ and s)

Answer 31

The fivenumber summary is usually better than the mean and standard deviation for describing a skewed distribution or a distribution with strong outliers. Use x̄ and s only for reasonably symmetric distributions that are free of outliers.

Question 32

what should you do when you find an outlier?

Answer 32

try to find an explanation for it

Question 33

What is the four step process?

Answer 33

1. STATE: What is the practical question, in the context of the real-world setting?
2. PLAN: What specific statistical operations does this problem call for?
3. SOLVE: Make the graphs and carry out the calculations needed for this problem.
4. CONCLUDE: Give your practical conclusion in the setting of the real-world problem.