chapter 18: Inference in practice

Question 1

The “simple conditions” are what…

Answer 1

1. We have a simple random sample (SRS) from the population of interest. There is no nonresponse or other practical difficulty. The population is large compared to the size of the sample.
2. The variable we measure has an exactly Normal distribution N(μ, σ) in the population.
3. We don’t know the population mean μ. But we do know the population standard deviation σ.

Question 2

The confidence interval of mean μ under simple conditions

Answer 2

Question 3

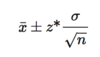
z-procedures: to test H₀: μ = μ₀, we use the one-sample z statistic:

Answer 3

The numerator measures how far the sample mean deviates from the hypothesized mean μ0. Larger values of the numerator give stronger evidence against H0: μ = μ0. The denominator is the standard deviation of ¯xx¯ . It measures how much random variation we expect. There is less variation when the number of observations n is large. So z gets larger (more significant) when the estimated effect ¯xx¯ − μ0 gets larger or when the number of observations n gets larger. Significance depends both on the size of the effect we observe and on the size of the sample.

Question 4

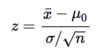
As you plan inference, you should always ask two questions

Answer 4

1. “Where did the data come from?”
2. “What is the shape of the population distribution?”

Question 5

statistical significance

Answer 5

the sample showed an effect larger than would often occur just by chance

Question 6

18.4 To obtain a desired margin of error m…

Answer 6

put in the value of z* for your desired confidence level, and solve for the sample size n

Question 7

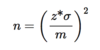
For a given effect size and level of significance, increasing sample size will ___________ power.

Answer 7

increase

Increasing sample size decreases the standard deviation of the sampling distribution, which results in rejecting a false null hypothesis more often.