Chapter 21: comparing two means

Question 1

two conditions for inference comparing two means

Answer 1

1. We have two SRSs, from two distinct populations. The samples are independent. That is, one sample has no influence on the other.
2. Both populations are Normally distributed.

Question 2

when do you use the hypothesis of no difference?

H₀: μ₁ = μ₂.

Answer 2

The hypothesis of no difference is used when investigating whether a treatment has an effect.

Question 3

how to make inferences about the differences between population means…

Answer 3

To make inferences about the difference μ₁ − μ₂ between the means of the two populations, we start from the difference x̄₁ − x̄₂ between the means of the two samples.

Question 4

how to find the standard deviation of the difference in sample means

Answer 4

This standard deviation gets larger as either population gets more variable, that is, as σ₁ or σ₂ increases. It gets smaller as the sample sizes n₁ and n₂ increase.

Question 5

how to find the standard error, or estimated standard deviation, when we don’t know the poputlation standard deviations

Answer 5

Because we don’t know the population standard deviations, we estimate them by the sample standard deviations from our two samples. The result is the standard error, or estimated standard deviation, of the difference in sample means

Question 6

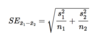
how to find the two-sample t-statistic

Answer 6

standardize the estimate by dividing it by its standard error

Question 7

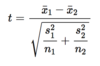
what does statistic t say

Answer 7

The statistic t has the same interpretation as any z or t statistic: it says how far x̄₁ − x̄₂ is from 0 in standard error units.

Question 8

how to determine a level C confidence interval for μ₁ − μ₂