Week 6 Flashcards
The number of fish in a small pond can be modelled using N=N0ekt where N is the number of fish t months after the start of the year and N0 is the number of fish in the pond at the start of the year.
If there were 50 fish in the pond at the start of the year and 70 fish three months later, calculate the growth factor k to four decimal places
The number of fish in a small pond can be modelled using N=N0ekt where N is the number of fish t months after the start of the year and N0 is the number of fish in the pond at the start of the year.
Using the model, predict the number of the fish in the pond at the start of August.
k=0.1122 No=50
The number of fish in a small pond can be modelled using N=N0ekt where N is the number of fish t months after the start of the year and N0 is the number of fish in the pond at the start of the year.
When would there be 150 fish in the pond?
k=0.1122 No=50
An amount of radioactive substance remaining can be modelled using N=N0ekt where N amount of radioactive substance remaining (measured in grams) and t is the number of years that has passed. There was initially 15 grams of radioactive substance, but only 10grams 60 years later.
Calculate the decay factor k to four decimal places.
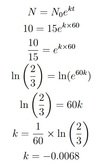
An amount of radioactive substance remaining can be modelled using N=N0ekt where N amount of radioactive substance remaining (measured in grams) and t is the number of years that has passed. There was initially 15 grams of radioactive substance, but only 10grams 60 years later.
Determine the half-life of the radioactive substance. The half-life is the time it takes for half of the radioactive substance to decay.
k= -0.0068
The population, P, of a certain variety of fish introduced into a dam can be modelled using P= 400×100.08t where t is the number of months after the introduction of fish to the dam.
Using the model, determine the number of fish in the pond after 3 months.
N= 400×100.08×3
= 695.12
After three months there will be approximately 695 fish in the dam.
The population, P, of a certain variety of fish introduced into a dam can be modelled using P= 400×100.08t where t is the number of months after the introduction of fish to the dam.
Using the model, determine the number of fish in the pond after 8 months.
N= 400×100.08×8
= 1746.06
After eight months there will be approximately 1746 fish in the dam.
The population, P, of a certain variety of fish introduced into a dam can be modelled using P= 400×100.08t where t is the number of months after the introduction of fish to the dam.
How long will it take for the number of fish in the dam to reach 5000?
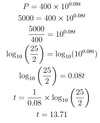
The population, P, of a certain variety of fish introduced into a dam can be modelled using P= 400×100.08t where t is the number of months after the introduction of fish to the dam.
What is the minimum number of fish in the dam? When does this occur?
As the fish population can be modelled using an exponential growth model, the number of fish will continue to increase. Therefore, the minimum number of fish in the dam is 400 which occurs when the fish were first introduced into the dam (t= 0).
A model for population growth in Australia is N= 19×1.015t where N is the population in millions and t is the number of years since the beginning of the year 2000.
What was Australia’s population at the start of 2000?
N= 19×1.0150
= 19
Australia’s population was 19 million at the start of 2000
A model for population growth in Australia is N= 19×1.015t where N is the population in millions and t is the number of years since the beginning of the year 2000.
Using the model, predict Australia’s population in 2025
N= 19×1.01525
= 27.57
Australia’s population is predicted to be 27.57 million at the start of 2025
A model for population growth in Australia is N= 19×1.015t where N is the population in millions and t is the number of years since the beginning of the year 2000.
In what year is Australia’s population expected to reach 50 million?
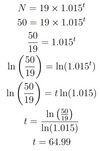
0◦≤θ≤360◦
sin(θ) =1/2
The first solution can be obtained from the special triangles:θ= 30◦. Another solution can be found in the second quadrant (as sin is positive in the second quadrant). This gives θ= 150◦. Therefore the two solutions areθ= 30◦ and θ= 150◦.
0◦≤θ≤360◦
tan(θ) =1/√3
The first solution can be obtained from the special triangles:θ= 30◦. Another solution can be found in the third quadrant (as tan is positive in the third quadrant). This gives θ= 210◦. Therefore the two solutions are θ= 30◦ and θ= 210◦.
0◦≤θ≤360◦
√2cos(θ)−1 = 0
0◦≤θ≤360◦
2sin(θ)−√3 = 0
0≤x≤2π. Give your answers as exact values.
10cos(x) = 5
0≤x≤2π. Give your answers as exact values.
√2 sin(x) = 1
0≤x≤2π. Give your answers as exact values.
√2 tan(θ) =√6
0≤x≤2π. Give your answers as exact values.
sin(x) = cos(x)
0◦≤θ≤360◦
sin(θ) =−1/2
0◦≤θ≤360◦
os(θ) =−√3/2
−π≤x≤π. Give your answers as exact values.
tan(x) =−1/√3
−π≤x≤π. Give your answers as exact values.
√10cos(x) +√5 = 0
π≤y≤2π. Round your answers to two decimal places.
5 tan(y)−2 = 0
π≤y≤2π. Round your answers to two decimal places.
10 cos(y) + 9 = 0
The population of an endangered frog colony living near a lagoon can be modelled by N= 16 + 98/t+2 where N is the number of frogs t weeks after a virus strikes the colony.
What was the frog population when the virus entered the colony?
The population of an endangered frog colony living near a lagoon can be modelled by N= 16 + 98/t+2 where N is the number of frogs t weeks after a virus strikes the colony.
What was the frog population 5 weeks after the virus entered the colony?
The population of an endangered frog colony living near a lagoon can be modelled by N= 16 + 98/t+2 where N is the number of frogs t weeks after a virus strikes the colony.
When does the frog population reach 18?
f(x) = 3x2+ 2x−1.
Evaluate f(4).
f(x) = 3x2+ 2x−1.
Evaluate f(−5).
f(x) = 3x2+ 2x−1.
Evaluate f(0)
f(x) = 3x2+ 2x−1
Find f(3a)
f(x) = 3x2+ 2x−1.
Find f(b+ 1)
