Week 5 Flashcards
5x+ 4 = 19
5x+ 4 = 19
5x+ 4−4 = 19−4
5x= 15
5x/5=15/5
x= 3


3x+ 9 =−3
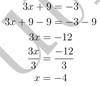
−2x+ 6 = 26
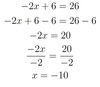
x/5 + 2 = 7
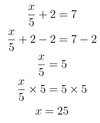
2x/3 − 4 = 0
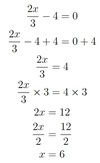
6n+ 8 = 44

5(3m−1) = 70

−18−3h= 5
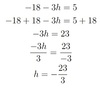
4x+ 7 = 8−x
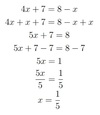
2(4y+ 1) = 5(3−y)
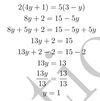
7(5−c) = 3(c+ 1)−10

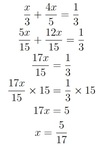
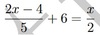

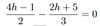
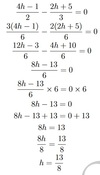
The kinetic energy, E, of an object is given by E=1/2mv2 where m is the mass of the object in kg and v is its velocity in m/s. Kinetic energy is measured in Joules (J).
Find the kinetic energy, E, of an object that has a mass of 8kg and is travelling at 6m/s.

The kinetic energy, E, of an object is given by E=1/2mv2 where m is the mass of the object in kg and v is its velocity in m/s. Kinetic energy is measured in Joules (J).
An object has a kinetic energy of 180J and is travelling at 8m/s. Find the mass of the object.
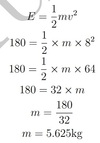
The kinetic energy, E, of an object is given by E=1/2mv2 where m is the mass of the object in kg and v is its velocity in m/s. Kinetic energy is measured in Joules (J).
Find the velocity of an object if it has a mass of 11.5kg and has a kinetic energy of 81.6J.
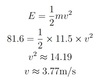
The surface area, S, of a box with length L, width W and height H is given by
S= 2(L×W) + 2(L×H) + 2(H×W).
Find the surface area of a box with a length of 5cm, width of 3cm and a height of 2.5cm.
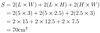
The surface area, S, of a box with length L, width W and height H is given by
S= 2(L×W) + 2(L×H) + 2(H×W).
Find the height of a box with a surface area of 154.78cm3, a length of 8.5cm and a width of 4.4cm.

n2−4n= 0
n2−4n= 0
n(n−4) = 0
n= 0, n= 4
3h2−27 = 0
3h2−27 = 0
3(h2−9) = 0
3(h−3)(h+ 3) = 0
h= 3, h=−3
k2−13k+ 42 = 0
k2−13k+ 42 = 0
(k−6)(k−7) = 0
k= 6, k= 7
3x2+x−2 = 0
3x2+x−2 = 0
(3x−2)(x+ 1) = 0
x=2/3, x=−1
2a2= 5a+ 3
2a2= 5a+ 3
2a2−5a−3 = 0
(2a+ 1)(a−3) = 0
a=−1/2, a= 3
9y2= 4
9y2= 4
y2=4/9
y=±√4/9
y=±2/3
or
y=−2/3, y=2/3
2x2+ 4x−6 = 0
2x2+ 4x−6 = 0
2(x2+ 2x−3) = 0
x2+ 2x−3 = 0
(x+ 3)(x−1) = 0
x=−3, x= 1
p2= 7p−4
p2= 7p−4
p2−7p+ 4 = 0
This quadratic does not factorise easily. Therefore it is necessary to use the quadratic formula.
p=7±√(−7)2−4×1×4/2×1
=7±√33 /2
2x2−9x+ 5 = 0
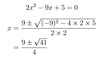
5x2−3x−1 = 0

Twice a number is added to 3 times its square. The result is 16. What was the original number?

A soccer ball is kicked such that its height, h, above the ground t seconds after it is kicked is given by h=−t(t−6). How long after it is kicked does it hit the ground?
The equation for the height (h) of the ball t seconds after it has been kicked is given by
h=−t(t−6)
To find when the ball hits the ground, let h= 0. This gives
0 =−t(t−6)
The solutions to this quadratic are t= 0 and t= 6. If we assume that the ball was on the ground at t= 0 and then kicked into the air, the ball will hit the ground six seconds after it has been kicked.
log2(x) = 4
log2(x) = 4
x= 24
x= 16
log5(x) = 3
log5(x) = 3
x= 53
x= 125
6 log4(x) = 12
6 log4(x) = 12
log4(x) = 2
x= 42
x= 16
log3(x) + 7 = 10
log3(x) + 7 = 10
log3(x) = 3
x= 33
x= 27
log10(5x) = 2
log10(5x) = 2
5x= 102
5x= 100
x= 20
4 log7(9x) = 8
4 log7(9x) = 8
log7(9x) = 2
9x= 72
9x= 49
x=49/9
8 log2(4x) = 24
8 log2(4x) = 24
log2(4x) = 3
4x= 23
4x= 8
x= 2
5 log3(6x−1) = 10
5 log3(6x−1) = 10
log3(6x−1) = 2
6x−1 = 32
6x−1 = 9
6x= 10
x=10/6
x=5/3
9 log5(3x+ 2) + 7 = 25
9 log5(3x+ 2) + 7 = 25
9 log5(3x+ 2) = 18
log5(3x+ 2) = 2
3x+ 2 = 52
3x+ 2 = 25
3x= 23
x=23/3
3 log4(5x+ 8)−4 = 2
3 log4(5x+ 8)−4 = 2
3 log4(5x+ 8) = 6
log4(5x+ 8) = 2
5x+ 8 = 42
5x+ 8 = 16
5x= 8
x=8/5
2x= 12
This question could be solved with logarithms of any base. The obvious choices are base 2, base 10 and base e. The solutions for base 2 are shown below.
Using base 2 logarithms:
2x = 12
log2(2x) = log2(12)
x * log2(2) = log2(12)
x * 1 = log2(12)
x = log2(12)
However, the question asked us to round our answer to two decimal places. To do this,we will need to use the change of base rule.
x= log2(12)
=log10(12)/log10(2)
= 3.58
5x= 30
5x= 30
log10(5x) = log10(30)
x × log10(5) = log10(30)
x=log10(30)/log10(5)
x= 2.11
9x= 58
9x= 58
log10(9x) = log10(58)
x×log10(9) = log10(58)
x=log10(58)/log10(9)
x= 1.85
ex= 4
ex= 4
ln(ex) = ln(4)
x×ln(e) = ln(4)
x= 1.39
2ex= 12
2ex= 12
ex= 6
ln(ex) = ln(6)
x×ln(e) = ln(6)
x= 1.79
7ex= 21
7ex= 21
ex= 3
ln(ex) = ln(3)
x×ln(e) = ln(3)
x= 1.10
5ex+ 4 = 14
5ex+ 4 = 14
5ex= 10
ex= 2
ln(ex) = ln(2)
x×ln(e) = ln(2)
x= 0.69
3e2x+1= 15
3e2x+1= 15
e2x+1= 5
ln(e2x+1) = ln(5)
(2x+ 1)×ln(e) = ln(5)
2x+ 1 = ln(5)
2x= ln(5)−1
x=ln(5)−1/2
x= 0.30
8e5x−4= 32
8e5x−4= 32
e5x−4= 4
ln(e5x−4) = ln(4)
(5x−4)×ln(e) = ln(4)
5x−4 = ln(4)
5x= ln(4) + 4
x=ln(4)+4/5
x= 1.08
6e9x+7+ 2 = 20
6e9x+7+ 2 = 20
6e9x+7= 18
e9x+7= 3
ln(e9x+7) = ln(3)
(9x+ 7)×ln(e) = ln(3)
9x+ 7 = ln(3)
9x= ln(3)−7
x=ln(3)−7/9
x=−0.66
The mass, m, of a baby animal (in kg) t weeks after it is born can be modelled by
m= 3 log10(8t+ 10)
Find the mass of the animal when it is born.
m= 3 log10(8t+ 10)
To find the mass of the animal at birth, substitute t= 0 into the equation form. (This is because it has been zero weeks since its birth).
m= 3 log10(8×0 + 10)
= 3 log10(10)
= 3 kg
The mass, m, of a baby animal (in kg) t weeks after it is born can be modelled by
m= 3 log10(8t+ 10)
Find the mass of the animal 10 weeks after it was born
m= 3 log10(8t+ 10)
m= 3 log10(8×10 + 10)
= 3 log10(90)
≈5.86 kg
The mass, m, of a baby animal (in kg) t weeks after it is born can be modelled by
m= 3 log10(8t+ 10)
How long until the animal is 8kg?

32x−4×3x+ 4 = 0



