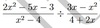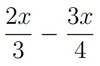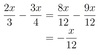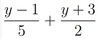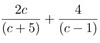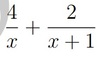Week 4 Flashcards
-5m(2n - 3m) … Can variables be distributed when simplifying?
Yes: -10mn + 15m^2
(6c + 12d) - (10c - 5d) Solution to coefficient of “c” signed or unsigned? Why?
Subtraction is not Commutative thus: (6c) - (10c) = -4c
(-12) - (-4) means: (+4) OR (-4) ?
+4 double - turns + (-12) + (-4) is the same as (-4)
2n(3n+ 1)(4n+ 2) make into quadratic
Expand the brackets and times by 2n as a whole after = 2n[12n^2+ 6n+ 4n+ 2] = 2n[12n^2+ 10n+ 2] = 24n^3+ 20n^2+ 4n Also can mult by 2n first
(2c+ 3)(c−1)(c+ 2) Use foil
Foil first two then foil for remaining two = (2c^2−2c+ 3c−3)(c+ 2) = (2c^2+c−3)(c+ 2) = 2c^3+ 4c^2+c^2+ 2c−3c−6 = 2c^3+ 5c^2−c−6
13x−(5x−2)(1−x)
keep parans until fully resolved arrange parans into quadratic = 13x −(5x −5x^2 −2 + 2x) = 13x −(−5x^2 + 7x −2) = 13x + 5x^2 −7x + 2 = 5x^2 + 6x + 2
(√7y)(√7y)
Root is negated variable stacks = 7y^2
-√7y -√7y
Surds stack -2√7y
(4−2a)(4 + 2a) does foil work?
Difference of two squares Foil only gets incomplete answer, must add the index if foil doesnt get that = 4^2−(2a)^2 = 16−4a^2
−(x−9)(x+ 9) What does - do?
Minus is applied to the signing of each term. = −(x^2−9^2) = −(x^2−81) = −x^2+81
1960 Prime factorise
repeated division of lowest factor 2 | 1960 2 | 980 2 | 490 5 | 245 7 | 49 7 | 7 1 stop at prime
HCF? 2 | 1960 2 | 1512 2 | 980 2 | 756 2 | 490 2 | 378 5 | 245 3 | 189 7 | 49 3 | 63 7 | 7 3 | 21 1 7 | 7 1
product of like factors 2^3 * 7 = 56
4a^3+12a^2 factorise
4a^2(a+3)
8-2n^2 factorise
2(4-n^2) factor out 2(2-n)(2+n) DOTS
0.01-x^2 factorise
0.1^2 = 0.01 thus (0.1-x)(0.1+x)
4nm^2-256n factorise
4n(m^2-64) factor out 4n(m-8)(m+8) DOTS
11-k^2 factorise
root to surd (√11+k)(√11-k)
2n^2+14n+20 factorise
Before using crossfire first the coefficient must be factored out 2(n^2+7n+10) then crossfire 2(n+5)(n+2)
-x^2-8x-12 factorise
-(x^2-8x-12) factor out crossfire since theres subtraction at head, the answers +6 & +2 can be used with the sub preserved: -(x+6)(x+2)
4m^2+2m-6 factorise
2(2m^2+m-3) crossfire 2(2m+3)(m-1)
y^4−28y^2+ 75 factorise
To make this easier to factorise, let A=y^2 = A^2−28A+ 75 substitute = (A−3)(A−25) crossfire = (y^2−3)(y^2−25) unsubstitute = (y^2−3)(y+ 5)(y−5) DOTS
(a+ 3)^2+ 8(a+ 3) + 12
= B^2+ 8B+ 12 = (B+ 2)(B+ 6) = ((a+ 3) + 2)((a+ 3) + 6) = (a+ 5)(a+ 9)
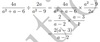
y-1/5 + y+3/2
= 2y-2/10 + 5y+15/10 = 7y+13/10
2c/(c+5) + 4/(c-1)
Q. 2c/(c+5) + 4/(c-1) = 2c(c-1)/(c+5)(c-1) + 4(c+5)/(c+5)(c-1) = 2c(c-1)+4(c+5)/(c+5)(c-1) = 2c^2-2c+4c+20/(c-1)(c+5) = 2c^2+2c+20/(c-1)(c+5) This is complete, quad wont factorise further
n+1/n+2 - 2n+1/3n-2 factorise
Q. n+1/n+2 - 2n+1/3n-2 = (n+1)(3n-2)/(n+2)(3n-2) - (2n+1)(n+2)/(n+2)93n-2) = (n+1)(3n-2) - (2n+1)(n+2)/(n+2)(3n-2) = 3n^2-2n+3n-2-(2n^2+4n+n+2)/(n+2)(3n-2) = 3n^2+n-2-2n^2-5n-2/(n+2)(3n-2) = n^2-4n-4/(n+2)(3n-2)
x/25 * 10/y
Q: x/25 * 10/y = x/5 * 2/y = 2x/5y
20/21a * 7c/10
Q: 20/21a * 7c/10 = 2/3a * c/1 = 2c/3a
3nm/5 / 9n/10
note: variable n cancels Q: 3nm/5 / 9n/10 = 3nm/5 * 10/9n = m/1 * 2/3 = 2m/3
Q: x-7/1-x^2 / 2x-14/x+1
Q: x-7/1-x^2 / 2x-14/x+1 = x-7/1-x^2 * x+1/2x-14 = x-7/(1+x)(1-x) * x+1/2(x-7) = 1/1-x * 1/2 = 1/2(1-x)
−3(a+ 6)
−3(a+ 6)
= −3a−18
2(2h+ 4k)
2(2h+ 4k)
= 4h+ 8k
−5m(2n−3m)
−5m(2n−3m)
=−10mn+ 15m2
4(x+ 2y) + 2(2x−y)
4(x+ 2y) + 2(2x−y)
= 4x+ 8y+ 4x−2y
= 8x+ 6y
6(c+ 2d)−5(2c+d)
6(c+ 2d)−5(2c+d)
= 6c+ 12d−10c−5d
=−4c+ 7d
2a+b−3(a−2b)
2a+b−3(a−2b)
= 2a+b−3a+ 6b
= −a+ 7b
−2(n−4)−(3n+ 1)
x(2x−3) + 4(x2+ 2)
x(2x−3) + 4(x2+ 2)
= 2x2−3x+ 4x2+ 8
= 6x2−3x+ 8
2a(5a−1) + 3(4a+ 2)
2a(5a−1) + 3(4a+ 2)
= 10a2−2a+ 12a+ 6
= 10a2+ 10a+ 6
2g(1−2g)−5(g−2)
2g(1−2g)−5(g−2)
= 2g−4g2−5g+ 10
=−4g2−3g+ 10
4(x−3)−2(x−2)
4(x−3)−2(x−2)
= 4x−12−2x+ 4
= 2x−8
12(n−3) +n(−2−2n)
12(n−3) +n(−2−2n)
= 12n−36−2n−2n2
=−2n2+ 10n−36
(a+ 4)2
(a+ 4)2
= (a+ 4)(a+ 4)
=a2+ 4a+ 4a+ 16
=a2+ 8a+ 16
Alternatively, this could be expanded by
i. Squaring the first term: a2
ii. Twice the product of the terms: 2×a×4 = 8a
iii. Squaring the second term: 42= 16
(2x−3)2
(2x−3)2
= (2x−3)(2x−3)
= 4x2−6x−6x+ 9
= 4x2−12x+ 9
(y−√7)2
(y−√7)2
= (y−√7)(y−√7)
=y2−y√7−y√7 + 7
=y2−2y√7 + 7
Alternatively, this can also be written as y2−2√7y+ 7.
Note that in the second term,the square root sign is only over the 7 and not they. When writing this by hand,make sure that it is clear what is under the square root sign.
(n+ 6)(n−6)
(n+ 6)(n−6)
=n2−6n+ 6n−36
=n2−36
(4−2a)(4 + 2a)
(4−2a)(4 + 2a)
= 16 + 8a−8a−4a2
= 16−4a2
Alternatively, this can also be written as −4a2+ 16
−(x−9)(x+ 9)
−(x−9)(x+ 9)
=−(x2+ 9x−9x−81)
=−(x2−81)
=−x2+ 81
(x−4)(x−5)
(x−4)(x−5)
= x2−5x−4x+ 20
= x2−9x+ 20
(2y+ 7)(4y−1)
(2y+ 7)(4y−1)
= 8y2−2y+ 28y−7
= 8y2+ 26y−7
(3b+ 8)(10b−3)
(3b+ 8)(10b−3)
= 30b2−9b+ 80b−24
= 30b2+ 71b−24
(7h−2)(3h−5)
(7h−2)(3h−5)
= 21h2−35h−6h+ 10
= 21h2−41h+ 10
(a−2)(a+ 5)
(a−2)(a+ 5)
=a2+ 5a−2a−10
=a2+ 3a−10
(2x−1)(3x+ 4)
(2x−1)(3x+ 4)
= 6x2+ 8x−3x−4
= 6x2+ 5x−4
2n(3n+ 1) (4n+ 2)
[2n(3n+ 1)] (4n+ 2)
= 6n2+ 2n
= 24n3+ 12n2+ 8n2+ 4n
= 24n3+ 20n2+ 4n
or
2n[(3n+ 1)(4n+ 2)]
= 2n[12n2+ 6n+ 4n+ 2]
= 2n[12n2+ 10n+ 2]
= 24n3+ 20n2+ 4n
−5y(3−y)(y−2)
−5y(3−y)(y−2)
=−5y(3y−6−y2+ 2y)
=−5y(−y2+ 5y−6)
= 5y3−25y2+ 30y
(2c+ 3)(c−1)(c+ 2)
(2c+ 3)(c−1)(c+ 2)
= (2c2−2c+ 3c−3)(c+ 2)
= (2c2+c−3)(c+ 2)
= 2c3+ 4c2+c2+ 2c−3c−6
= 2c3+ 5c2−c−6
13x−(5x−2)(1−x)
13x−(5x−2)(1−x)
= 13x−(5x−5x2−2 + 2x)
= 13x−(−5x2+ 7x−2)
= 13x+ 5x2−7x+ 2
= 5x2+ 6x+ 2
(8 + 9h)(2h−3)
(8 + 9h)(2h−3)
= 16h−24 + 18h2−27h
= 18h2−11h−24
−2a(a+ 3)(a−3)
−2a(a+ 3)(a−3)
= −2a(a2−3a+ 3a−9)
= −2a(a2−9)
= −2a3+ 18a
x2−8x
x2−8x
= x(x−8)
4a3+ 12a2
4a3+ 12a2
= 4a2(a+ 3)
3a2b−15ab2
3a2b−15ab2
= 3ab(a−5b)
y2−9
y2−9 = (y+ 3)(y−3)
(Difference of two squares)
8−2n2
8−2n2
= 2(4−n2)
= 2(2 +n)(2−n)
1−x2
1−x2
= (1 +x)(1−x)
4nm2−256n
4nm2−256n
= 4n(m2−64)
= 4n(m+ 8)(m−8)
5x2−80
5x2−80
= 5(x2−16)
= 5(x+ 4)(x−4)
x2+ 5x+ 6
x2+ 5x+ 6
= (x+ 2)(x+ 3)
cross method
a2−11a−12
a2−11a−12
= (a−12)(a+ 1)
cross
y2−9y+ 20
y2−9y+ 20
= (y−4)(y−5)
cross
2n2+ 14n+ 20
2n2+ 14n+ 20
= 2(n2+ 7n+ 10)
= 2(n+ 5)(n+ 2)
Note that while the cross method has been used, the first step was to factorise usinga common factor. This made the cross method much easier.
3k2+ 33k+ 30
3k2+ 33k+ 30
= 3(k2+ 11k+ 10)
= 3(k+ 1)(k+ 10)
cross
−x2−8x−12
−x2−8x−12
=−(x2+ 8x+ 12)
=−(x+ 2)(x+ 6)
As all terms were negative, a common factor of −1 was first introduced. This allowed for the cross method to be used where all terms were positive.
5c2+ 105c+ 100
5c2+ 105c+ 100
= 5(c2+ 21c+ 20)
= 5(c+ 1)(c+ 20)
4m2+ 2m−6
4m2+ 2m−6
= 2(2m2+m−3)
= 2(2m+ 3)(m−1)
y4−28y2+ 75
We have been asked to factorise y4−28y2+ 75. This question could be done several different ways. To make it easier to factorise,
let A=y2
y4−28y2+ 75
= A2−28A+ 75
= (A−3)(A−25)
= (y2−3)(y2−25)
= (y2−3)(y+ 5)(y−5)
(a+ 3)2+ 8(a+ 3) + 12
We have been asked to factorise (a+ 3)2+ 8(a+ 3) + 12. To make it easier to factorise,let B= (a+ 3)
(a+ 3)2+ 8(a+ 3) + 12
=B2+ 8B+ 12
= (B+ 2)(B+ 6)
= ((a+ 3) + 2)((a+ 3) + 6)
= (a+ 5)(a+ 9)
Alternatively, you could expand, simplify, and then factorise.
(a+ 3)2+ 8(a+ 3) + 12
=a2+ 6a+ 9 + 8a+ 24 + 12
=a2+ 14a+ 45
= (a+ 5)(a+ 9)
