Week 1 Flashcards
(54 cards)
percentage -> fraction
/100
fraction -> percentage
*100
decimal -> percentage
*100
fraction -> decimal
N/D
decimal -> fraction
decimal (a.bc…) = a bc/100
Natural Numbers (N)?
(also called positive integers, counting numbers, or natural numbers); They are the numbers {1, 2, 3, 4, 5, …}
Whole Numbers (W).
This is the set of natural numbers, plus zero, i.e., {0, 1, 2, 3, 4, 5, …}.
Integers (Z).
This is the set of all whole numbers plus all the negatives (or opposites) of the natural numbers, i.e., {… , ⁻2, ⁻1, 0, 1, 2, …}
Rational numbers (Q).
This is all the fractions where the top and bottom numbers are integers; e.g., 1/2, 3/4, 7/2, ⁻4/3, 4/1 [Note: The denominator cannot be 0, but the numerator can be].
Real numbers (R),
(also called measuring numbers or measurement numbers). This includes all numbers that can be written as a decimal. This includes fractions written in decimal form e.g., 0.5, 0.75 2.35, ⁻0.073, 0.3333, or 2.142857. It also includes all the irrational numbers such as π, √2 etc. Every real number corresponds to a point on the number line.
Discrete and continuous numbers?
Discrete:
Natural, Whole, Integers, Rationals
This means that they are separate and distinct entities. In fact each of these sets is countable.
Continuous:
Real numbers cannot be counted. This is because they are continuous. Between any two real numbers, however close they may be, there are infinitely more real numbers.
e
e=(1 + 1/n)^n
3/6i
i is in the Den
Rationalize the Denominator
= 3*i/6i*i
= 3i/-6
= i/-2 OR - i/2 OR - 1/2 i
Index Laws?
Mult
Div
Powpow
Fractional
an * am = an+m
an / am = an-m
(an)p = an*p
ax/y = y√ax
Index Laws?
Negative
Zero
Advanced (4)
a-n = 1/an
a0 = 1
ap/q = q√ap = (a1/q)p
25^1/2
√25 = 5
-2^4
expand
-(2*2*2*2) = -16
NOT
(−2)*(−2)*(−2)*(−2) = 16
4 - 3 1/8
??? fix
7/8
OR
0.78
5127 * 4265
align
5127
4265
25635
(5 * all)
5127
4265
25635
(6 * all) (add 0)
307620
5127
4265
25635
307620
(2 * all) (add 00)
1025400
ETC…
THEN ADD ALL PRODUCTS:
5127
4265
_____
25635
307620
1025400
20508000
_________
21866655
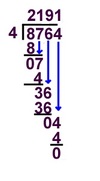
Long Division?
Dividend / Divisor = Quotient
Quotient
Divisor (Dividend
8764 / 4
10π/5
2π
10π/5π = 2
the number e can be calculated by adding and infinite number of terms of:
1 + 1/1 + 1/1*2 + 1/1*2*3 + 1/1*2*3*4 …
add each of the first 6 terms as decimals to 5 decimal plaveces. Add these 6 terms to get an approximate value of e
4√20 - 2√5
Q: 4√20 - 2√5
= 4 * √4 * √5 - 2√5
= 4 * 2 * √5 - 2√5
= 8√5 - 2√5
= 6√5


