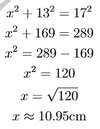Week 2 Flashcards
log4(16)
= 2 (as 4^2= 16)
log2(8)
log2(8) = 3(as 2^3= 8)
log5(125)
log5(125) = 3(as 5^3= 125)
log9(1)
log9(1) = 0(as 9^0= 1)
log3(1/3)
log3(1/3)
= log3(3−1)
= −1×log3(3)
= −1×1
= −1
log5(1/25)
log5(1/25)
= log5(1/52)
= log5(5−2)
= −2×log5(5)
= −2×1
= −2
log12(6) + log12(2)
log12(6) + log12(2)
= log12(6×2)
= log12(12)
= 1
log8(2) + log8(4)
log8(2) + log8(4)
= log8(2×4)
= log8(8)
= 1
log6(3) + log6(12)
log6(3) + log6(12)
= log6(3×12)
= log6(36)
= 2
log4(1/2) + log4(32)
log4(1/2) + log4(32)
= log4(1/2 * 32)
= log4(16)
= 2
log5(8) + log5(1/8)
log5(8) + log5(1/8)
= log5(8 * 1/8)
= log5(1)
= 0
log3(54)−log3(6)
log3(54)−log3(6)
= log3(54/6)
= log3(9)
= 2
log5(250)−log5(2)
log5(250)−log5(2)
= log5(250/2)
= log5(125)
= 3
log9(90)−log9(5)−log9(2)
log9(90)−log9(5)−log9(2)
= log9(90/5)−log9(2)
= log9(18)−log9(2)
= log9(18/2)
= log9(9)
= 1
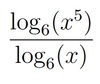
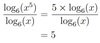

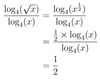
log10(123)
log10(123) = 2.0899
ln(8)
ln(8) = 2.0794
log5(60)
log5(60)
=log10(60)/log10(5)
= 2.5440
log7(25)
log7(25)
=log10(25)/log10(7)
= 1.6542
log2(18)
log2(18)
=log10(18)/log10(2)
= 4.1699
log9(2)
log9(2)
= log10(2)/log10(9)
= 0.3155


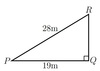

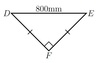

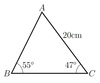

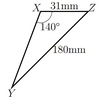



Find all unknown side lengths and angles in the following triangle
In triangleABC,a= 23.6cm,b= 12.3cm,c= 26.8cm

Find all unknown side lengths and angles in the following triangle
In triangleSTU, s= 17mm,u= 9mm, angleT= 118◦

Find all unknown side lengths and angles in the following triangle
In triangle PQR, q= 19cm, r= 16cm, angleQ= 56◦

A 4m ladder is leaning against a wall. The vertical distance from the top of the ladder tothe floor is twice the distance from the base of the ladder to the wall. Find the verticaldistance between the top of the ladder and the floor. Assume that the wall is perpendicularto the floor.

From where I stand, the angle from the ground to the top of a building (called the angleof elevation) is 50◦. I then walk 25m closer and the angle of elevation is now 65◦. What isthe height of the building?

A river runs in the East-West direction. Standing on the bank of the river, I take a bearingof 42◦to a jetty on the opposite bank. I then walk east for 120m and the bearing isnow 308◦. How wide is the river? (Hint: Remember that bearings are measured clockwise,starting from North)

A ship sails on a bearing of 210◦for 15km. It then changes direction and sails for 22kmand drops anchor. Its bearing from the starting point is 280◦. On what bearing did theship sail the second part of its journey (22km)?

A hockey goal is 3m wide. When a player is 7.2m from one goal post and 5.8m from theother she takes a shot at the goal. Within what angle must the shot be made to score the goal?

Two cars depart from the same point at noon. The angle between the two cars’ directionsis 78◦. One car travels at 100km/h and the other travels at 96km/h. What is the distancebetween the two cars at 2:15pm?

A boat travels on a bearing of 60◦for 5km. It then changes its course and travels East for10km.
How far is the boat from its starting position?

log2(16)
log2(16)
= log2(24)
= 4
log6(2) + log6(18)
log6(2) + log6(18)
= log6(2×18)
= log6(36)
= log6(6^2)
= 2
log5(50)−log5(2)
log5(50)−log5(2)
= log5(50/2)
= log5(25)
= log5(5^2)
= 2