Statistics

Question 1

What is an average or mean and how is it calculated?

Answer 1

The average or mean is an estimate of the value most representative of the population. This is often called the central tendency of the data. The computation of the mean ( X ) of a data set containing N values is given in the equation below:

Question 2

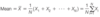
What is a median?

Answer 2

The median, another measure of central tendency, is the value between the lower half and the upper half of the population (the middle value for a data set).

Question 3

Of mean, median and mode, which is the most sensitive to extreme values or outliers?

Answer 3

Mean is sensitive to extreme values or outliers.

The mean is insufficient to describe the central tendency of all distributions.

Median is unaffected or only slightly affected.

Question 4

What is the mode in a data set?

Answer 4

The mode is the most frequently occurring number in a group of numbers.

Question 5

What is variance and how is it calculated?

Answer 5

Variance (V_x²), the difference between each point and the mean, and each difference is squared to keep all terms positive. Then the sum is divided by one less than the number of data points.

Question 6

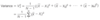
What is standard deviation and how is it calculated?

Answer 6

In statistics, the standard deviation (SD, also represented by the lower case Greek letter sigma σ) is a measure that is used to quantify the amount of variation or dispersion of a set of data values (i.e. how spread out the numbers in the data set are). A low standard deviation indicates that the data points tend to be close to the mean (also called the expected value) of the set, while a high standard deviation indicates that the data points are spread out over a wider range of values.

Question 7

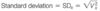
Explain step 1 for determining the standard deviation for a population data set.

Answer 7

Question 8

Explain step 2 for determining the standard deviation for a population data set.

Answer 8

Question 9

Explain step 3 for determining the standard deviation for a population data set.

Answer 9

Question 10

Explain step 4 for determining the standard deviation for a population data set.

Answer 10

Question 11

What does standard deviation tell us?

Answer 11

Question 12

How does the formula for standard deviation for a sample differ from the formula for standard deviation for a population?

Answer 12

Question 13

What are the formulas for standard deviation for a sample and for standard deviation for a population?

Answer 13