Sampling Variability and Confidence Intervals

Question 1

statistical inference

Answer 1

forming judgements about population parameters on the basis of sample data

parameter - summarizes a variable in a population (e.g. mean (μ), proportions (p)

statistic - summarizes a variable in a sample (e.g. mean (x), proportions (p))

Question 2

Suppose you took a total of 10,000 random samples of size n from a population with mean and standard deviation

Answer 2

Q: if you graphed the 10,000 values of x̅ from the samples, what would the graph look like?

A1: Centre - You would find that the mean of the sampling distribution of x̅ is equal to the mean of the population distribution 𝜇_𝑥̅= 𝜇 and we say that x̅ is an unbiased estimator of 𝜇

A2: Spread - You would find that the standard deviation (spread) of the 10,000 values of x̅ is narrower than the spread of the population distribution (i.e., sample averages are less variable than individual observations)

– You would also find that as n increases, the spread of the sampling distribution gets narrower (i.e., large samples are less variable than small samples) – specifically

𝜎_𝑥̅= 𝜎 / √n

This is called the standard error of the mean

A3: Shape – You would find that the shape of the sampling distribution of x̅ depends on the shape of the population

– If the population from which you took your sample is normal, then the shape of the sampling distribution of x̅is also normal

– If the population from which you took your sample is skewed, then the shape of the sampling distribution is less skewed

Question 3

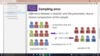
sampling error

Answer 3

difference between a statistic and the parameter, due to chance composition of the sample

ex) population: N=12; sample: n=8

proportion that are pink: P = 6/12 = 0.5; p = 5/8 = 0.63

sampling error = p - P = 0.13

Question 4

sampling variability

Answer 4

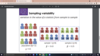
variation in the value of a statistic from sample to sample

population: N=12; P = 0.5

sample 1: n=8; p = 0.63

sample 2: n=8; p =0.25

Question 5

sampling distribution

Answer 5

a frequency distribution of a statistic, based on all possible samples of the same size from a population

population distribution

sampling distribution of sample means

Question 6

confidence interval

Answer 6

• A point estimate, because it is a single number, provides no information about the precision and reliability of estimation
• For example, the point estimate X̅ has sampling variability and provides no information about how close it might be to μ
• An alternative to calculating a single value is to calculate an entire range, or interval, of plausible values centred around X̅ – We hope that the interval contains the true, but unknown, value of μ
• A confidence interval (CI) is an interval estimate of a population parameter
• It is composed of:

a) An interval calculated from sample data The margin of error shows how accurate we believe our guess is based on the variability of the estimate
b) A confidence level (C) which gives the frequency of intervals that will capture the parameter in repeated samples of size n (e.g., 95% confidence interval)

Question 7

validity of confidence intervals

Answer 7

• The method of constructing confidence intervals rely on certain conditions:

a) Observations are from an unbiased sample

• no selection bias of unknown effect is present (e.g. non-response, measurement bias, etc.)

b) Assumed probability model is appropriate

• For means: observations must come from a population that is Normal OR sample size is large enough that Normal approximation is valid

Question 8

precision of confidence intervals

Answer 8

• Narrower confidence intervals (smaller margin of error) are more ‘precise’
• Precision can be increased by:

a) Sample size

• A larger sample size gives a smaller margin of error

b) Confidence level

• A lower confidence level gives a smaller margin of error