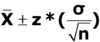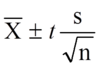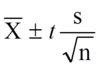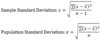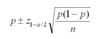Sampling and Estimation Flashcards
Simple Random Sampling
Selection of a sample such that each item of the population has the same likelihood of being included in the sample.
Systematic Sampling
Selection of every nth member from a population.
Sampling Error
The difference between a sample statistic (mean, variance, s-dev) and its corresponding population parameter.
Sampling Error of the mean
Sampling Distribution
Probability distribution of all possible sample statistics computed from a set of equal sized samples randomly selected from the same population.
Stratified random sampling
Use of a classification system to separate the population into smaller groups based on one or more distinguishing characteristics.
Time-series data
Observations taken over a period of time at specific and equally spaced time intervals.
Cross-sectional data
Sample of observations taken at a single point in time.
Longitudinal Data
Observatiosn over time of multiple characteristics of the same entity
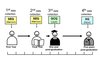
Panel data
Observations over time of the same characteristic for multiple entities
The size of the samples from each strata is based on the relative size of the strata relative to the population and not necessarily same across population
Classify the population into smaller groups based on one or more distinguishing characteristics
Take a random sample from each subgroup and pooled together.
The size of sample from each subgroup is based on relative of the group
Central Limit Theorem
For simple random samples of size n from a population with a mean of m and a finite variance, the sampling distribution of the same mean approaches a normal probability distribution with mean m and a variance equal to variance/n
Point estimates
Single (sample) values used to estimate population parameters.
Confidence interval
Confidence intervals are usually constructed by adding or subtracting an appropriate value from the point estimate
* Point Estimate +_ Reliability factor x Standard Error*
Range of values within which the actual value of a parameter will lie, given the probability of 1 - a
Level of significance
α
Degree of confidence
1 - α
Confidence interval form
Desirable properties of an estimator
Unbiasedness, efficiency, and consistency.
Desirable properties of an estimator - definitions
Student’s t-distribution
Bell-shaped probability distribution that is symmetrical about its mean.
Properties of student’s t-distribution
Confidence interval for the population mean (normal distribution with a known variance)
Commonly used standard normal distribution reliability factors
Confidence intervals for a population mean that is normal with unknown variance
Criteria for selecting the appropriate test statistic
Data Mining
Occurs when analysts use the same database to search fo rpatterns or trading rules until they discover one that “works.”
Data-mining bias
Results where the statistical significance of the pattern is overestimated because the results were found through data mining.
Sample selection bias
When some data is systematically excluded from the analysis because of lack of availability.
Survivorship bias
The most common bias… for example, when funds are no longer included because they have ceased to exist due to closure or merger.
Look-ahead bias
When a relationship is tested using sample data that was not availabe on the test date.
For example
Consider a test of a trading rule that is based on the price to book value
Stock Price
Are available for all companies at the same point of time
Book Value
While the year end book values may not be available for all companies until 30 to 60 days after the fiscal year ends
Time-period bias
Occurs when the time period over which the data was gathered is too short or too long.
Too Short
Results may reflect phenomenon specific to that time period or perhaps data mining
Too Large
The fundamental economic relationships that underlie the results may have changed
Desirable Properties of Estimator
1: - Unbiasedness
2: - Efficient
3: - Consistent
Unbiasedness
An unbiased estimator is one whose expected value equals the parameter it’s intended to estimate.
Expected Value
An unbiased estimator is one for which the expected value of the estimator is equal to parameter you are trying to estimate
For example because the expected value of the sample mean is equal to the population mean the sample mean is an unbiased estimator of the population mean
Efficiency
Enterprise Value
An estimator is efficient if no other estimator has a sample distribution with smaller variance.
An estimator is efficient if the variance of its sampling distribution is smaller the all of other unbiased estimators of the parameter you are trying to estimate
Consistency
Sample Size
Company Secretary
A consistent estimator is one for which the probability if estimates close to the value of the population parameter increases as sample size increases.
A consistent estimator is as you increase the sample size the accuracy of the parameter estimator also increases.
Therefore with an increase in the sample size the standard error of the sample mean also decrease and the sampling distribution bunches more closely around the population mean
As the sample size approaches infinity the standard error approaches zero
Confidence Interval
A 100(1-α)% confidence interval:
Point estimate +/- Reliability factor x Standard error.
Issues Regarding Selection of the Appropriate Sample Size
Limitations
1:-Larger samples may contain observations from a different from a different population (distribution)
2:-÷The cost of using a larger sample must be weighted against the value of the increase in the precision from the increase in sample size
Larger Sample Size Advantages
Larger Sample Size Advantages
1: -Reduces sampling error and standard deviation of the sample statistics around its population value
2: -Confidence intervals are narrower when samples are larger and the standard errors of the point estimates of population parameter are less
Sampling Error
Size of Samples in Stratified Random Sampling
The size of the samples from each strata is based on the relative size of the strata relative to the population and not necessarily same across population
Classify the population into smaller groups based on one or more distinguishing characteristics
Take a random sample from each subgroup and pooled together.
The size of sample from each subgroup is based on relative of the group
What is the probability of confidence interval ?
1- alpha
Alpha and 1 - Alpha
Confidence Interval estimates result in a range of values within which the actual of a parameter will lie given the probability of 1-alpha
Here alpha is called the level of significance for confidence interval
And the probability 1-alpha is referred to as the degree of confidence
Normal Distribution Classification
Non Normal Distribution Classification
Normal Distribution
Known Variance
Small Sample Size
Z Statistics
Interpretation
Probabilistic
After repeatedly taking samples of CFA candidates administering the practice exam and constructing confidence intervals for each sample’s mean 99% of the resulting confidence intervals will in the long run include the population mean
Practical
We are 99% Confident that the population mean score is between 73.5 and 86.45 for candidates from this population
Normal Distribution
Known Variance
Large Sample Size
Z Statistics
Interpretation
Probabilistic
After repeatedly taking samples of CFA candidates administering the practice exam and constructing confidence intervals for each sample’s mean 99% of the resulting confidence intervals will in the long run include the population mean
Practical
We are 99% Confident that the population mean score is between 73.5 and 86.45 for candidates from this population
Normal Distribution
UnKnown Variance
Small Sample Size
t-Statisitcs
Owing to the relatively fatter tails of the t-distribution confidence intervals constructed using reliability t-reliability factors will be more conservative (wider) than those constructed using z-reliability factors
Unlike the standard normal distribution the reliability factor for t-distribution depend on the sample size so we can’t rely on commonly used set if reliability factors
Normal Distribution
Unknown Variance
Large Sample Size
t-statistics
Owing to the relatively fatter tails of the t-distribution confidence intervals constructed using reliability t-reliability factors will be more conservative (wider) than those constructed using z-reliability factors
Unlike the standard normal distribution the reliability factor for t-distribution depend on the sample size so we can’t rely on commonly used set if reliability factors
Non Normal Distribution
Known Variance
Small Sample Size
NA
Non Normal Distribution
Known Variance
Large Sample Size
Z Statistics
If the distribution is non normal but the population variance is known the z statistics can be used as long as the sample size is large n is greater than 30
We do this because central limit theorem assures us that the distribution of the sample mean is approximately normal when the sample is large
Non Normal Distribution
UnKnown Variance
Small Sample Size
NA
Non Normal Distribution
UnKnown Variance
Large Sample Size
t-Statistics
It is also acceptable to use the z-statistics although use of the t-statistics is more conservative
If the distribution is non normal but the population variance is known the t-statistics can be used as long as the sample size is large n is greater than 30
Student’s t-distribution
It is a bell shaped probability distribution that is symmetrical about its mean
It is appropriate distribution to use when constructing confidence intervals based on small samples (n
It may also be appropriate to use the t-distribution when population variance is unknown and sample size is large enough that the central limit theorem will assure that the sample distribution is approximately normal
Student’s t-distribution
Properties
**Properties **
1: - Symmetrical
2: -Defined by single parameter the degrees of freedom where the degrees of freedom are equal to the number of sample observation minus one for sample mean
3: -It has more probability in the tails (fatter tails) than normal distribution
4: -As the degrees of freedom (the sample size ) the shape of the t-distribution more closely approaches a standard normal distribution
Standard Error
Standard Deviation is Equal to
Standard Error of the Sample Mean
The
Positive Square Root
of the
Variance
of the
Sample Statistics
What does Standard Error Truely Signify
Standard Deviation Formula for Square Root of Sum of Squared Deviation to the Mean
Time Period Bias
Can result if the time period over which the data is gathered is either too short or too large
Too Short:- Results may reflect phenomenon specific to that time period or perhaps data mining
When to use sample standard deviation and when to use population standard deviation in calculating standard error
When population standard deviation is given use that to calculate standard error but when it’s not given (population standard deviation) than use sample standard deviation.
How to identify whether to use t-distribution or z - distribution
See the sample size
See what is given standard deviation .
Sample or population
Formula Confidence Interval for Bernoulli Trial
Formula for Width of Confidence Interval
Properties of Central Limit Theorem
