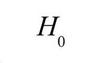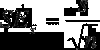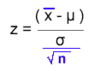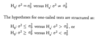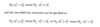Hypothesis Testing Flashcards
Hypothesis
statement about the value of a population parameter developed for purpose of testing a theory or belief
Hypothesis Testing Procedure (picture pg 298 book 1)
j
Null Hypothesis
Designated Hο, hypothesis that the researcher wants to reject. Actually texted and is basis for selection of test stat. Always “equal to” condition
Alternative Hypothesis
Há, what is concluded if there is sufficient evidence to reject the null. Usually alternative hypo trying to assess.
One-tailed Two-tailed
one - if return is greater than zero two - if research question is returns different from zero Hο:µ=µο vs Há:µnot=µο
Reject Hο if:
Test statistic > upper critical value or Test statistic < lower critical value
Hypo testing - two statistics
Test statistic calculated from sample data Critical value of test statistic
Test Statistic =
(Sample Stat - Hypo Value) / Standard error of sample stat
Type I Error
rejection of null hypo is actually true
Type II Error
Failure to reject the null hypothesis when actually false
Significance Level
The probability of making a Type I Error and designated alpha letter
Decision Rule
Based on the distribution of the test statistic. Must figure out one tail or two tails before decision rule -specific and quantitative -test statistic (greater / less than) X, reject the null
Power of a test
probability of correctly rejecting the null when it is false. 1-probability of making a Type II error, or 1-P (Type II error) Rejecting null when false (power of test) equals one minus the probability of NOT rejecting the null when it is false (type II error)
Level significance, power of a test, and type two errors. (pg 303 book 1 picture)
…
Decreasing significance level
(probability of type II error) will increase probability of failing to reject the null, and decreasing power of test. and vice versa
Confidence Level (formula pg 304 book 1)
…
Confidence level interval
-critical value ≤ test statistic ≤ +critical value Range within which we fail to reject the null for a two-tailed test at a given level of significance
P-Value
Probability of obtaining a test statistic that would lead to a rejection of the null, assuming the null was true. -Smallest level of significance for which null can be rejected One tail- pval is probability that lies above the positive value of the computed test stat for upper tail tests, or below for lower tailed tests. Two tail -pval probability that lies above the positive val of the compound test stat plus the probaility that lies below the negative value of the computed test stat
T-Test Picture pg 307 book 1
employes a test stat that is distributed according to a t-distribution. Use if: Variance unknown sample is large (n≥30 Sample is small (less than 30) but distribution of population is normal
Z-Test picture pg 308 book 1
when population is normally distributed with a known variance Z val is compared to the significance of test.
Memorize this picture pg 308 book 1
…
When samples are independant
Use the difference in mean test
When samples are dependant
statistic is average difference in (paired) observations divided by the standard error of the average difference
Chi-square test
used for hypothesis tests concerning the variance of a normally distributed population. Distribution is asymmetrical and approaches the normal distribution in shape as the degrees of freedom increase
Hypothesis Testing :-Definition
- A Hypothesis is a statement about the value of a population parameter developed for the purpose of testing a theory or belief
- Hypothesis are stated in terms of the population parameter to be tested like the population mean
Null Hypothesis
- It is the hypothesis that the researcher wants to reject
- It is the hypothesis that is actually tested and is the basis for the selection of test statistics
- The null is generally stated as a simple statement about a population parameter
- The null hypothesis includes the equal the equal to condition
Alternative Hypothesis
- The alternative hypothesis is what is concluded if there is sufficient evidence to reject the null hypothesis
- Since you can never really prove anything with statistics when the null hypothesis is discredited the implication is that the alternate hypothesis is valid
Hypothesis Testing
Process
Hypothesis Testing Process
Some test Signify Divine and Collective Decision
Hypothesis Test
Hpothesis Test
Two Tailed Test
A two tailed test for population mean may be structured as
General Rule for 2 Tailed Hypothesis Test
Since the alternative hypothesis allows for values above and below the hypothesised parameter a two tailed test uses two critical values (or rejection point)
Structuring of General Rule for 2 Tailed Hypothesis Test
Example of 2 Tailed Test
One Tailed Test
Example One Tailed Test
Test Statistics
and
Hypothesis Test
Test Statistics
Hypothesis Testing involves two statistic
- The test statistics calculated from the data
- **The critical value of the test statistics **
The value of the computed test statistics relative to the critical value is the key step in assessing the validity of hypothesis
How is test statistics calculated
- A test statistics is calculated by comparing the point estimate of the population parameter with the hypothesised value of the parmeter
- The test statistics is the difference between the sample statistics and the hypothesised value scaled by the standard error of the sample statistics
Standard Error
The Standard Error of the sample mean is the adjusted standard deviation of the sample
When the sample statistic is the sample mean,x, the standard error of the sample statistic for sample size n is calculated as
When the population standard deviation sigma is known
When the population standard deviation sigma is not known
Distribution
A test statistics is a random variable that may follow one of several distributions depending on the characteristics of the sample and population
We will study 4 distribution for test statistics
- t-distribution
- z-distribution
- Chi-square distribution
- F-distribution
Power of test
- It is the probability of correctly rejecting the null hypothesis when it is false
- It is one minus the probability of making Type II Error or 1- P (Type II Error)
Power of Test Depends on
- Sample Size and
- Choice of significance level (Type I Error Probability ) will together determine the probability of a Type II Error
- Decreasing the significance level (probability of Type I Error ) from 5% to 1% for example will increase the probability of failing to reject the null hypothesis (type II error ) and therefor reduce the power of test
- Conversely for a given sample size we can increase the power of test only with the cost that the probability of rejecting a true null (type I error ) increases
- For a given significance level we can decrease the probability of a type II error and increase the power of test only by increasing the sample size
p-value
Significance Level
- The significance level is the probability of making a Type I Error (rejecting the null hypothesis when it’s true ) and is designated by Greek letter alpha
- For instance a significance level of 5% means there is 5% chance of rejecting a true null hypothesis
- p-value is the probability of obtaining a test statistics that would lead to a rejection of the null hypothesis assuming null hypothesis is true Type I Error
Classification of Test
Null Hypothesis Test is False
and Accepted
Type II Error
Null Hypothesis is False
and
Rejected
No Error
Power of Test
Null Hypothesis is True
Accepted
No Error
Null Hypothesis is True
Rejected
Type I Error
Null Hypothesis is True
Rejected
Null Hypothesis is False
Accepted
Null Hypothesis is True
Your Decision
Null Hypothesis is False
Type I Error Falsely Positive
When Null Hypothesis is True
and
Rejected
- Significance Level :- The significance level is the probability of making a Type I Error
- Rejecting the null hypothesis when it’s true is designated by Greek letter alpha
- For instance a significance level of 5% means there is 5% chance of rejecting a true null hypothesis
Null Hypothesis is False
and
Accepted
- Type II Error Falsely Negative
Null Hypothesis is False
and
Accepted
Type II Error
Standard Error Vs Sample Error
- Sampling Error of the Sample Mean
= Sample Mean - Population Mean
- Standard Error:-Standard error of the sample mean is the standard deviation of the distribution of the sample means
Type I and Type II Error
When hypothesis testing
the choice between using critical value based on the t-distribution or z-distribution depends on
- Sample Size
- the distribution of the population
- Whether or not the variance of population is known
The t-Test
- Brief :- The t-test is a widely used hypothesis test that employs a test statics that is distributed according to t-distribution.
- In the real world the underlying variance of the population is rarely known so the test enjoys widespread application
- Where to Use:- Use the t-test if the population variance is unknown and either of the following condition is met 1:-The sample size is large > 30 2:-The sample is small less than 30 but thedistribution of the population is normal or approximately normal
The t-Test
To conduct the t-test the t-statistics is compated to critical t-value at desired level of significance with the appropiate degrees of freedom
Formula
The z-Test
- Brief :-The z-test is the appropriate hypothesis test of the population mean when the population is normally distributed with known variance
The z-test
Formula
When the population variation is known
The z-Test
Formula when population variance is not known and the sample size is large enough
Note that use of sample standard deviation versus the population standard deviation .
Remember that this is acceptable if sample size is large although the t-statistics is more conservative measure when population deviation is not known.
The z-Test
Critical Values
The t-Test
- There are two distinct hypothesis tests 1) one about the significance of the difference between the means of two populations 2)and one about the significance of mean of the difference between pairs of observations Rules :-
- The test of the difference of means is used when there are two independent samples
- A test of the significance of the mean of the difference between paired observations is used when the samples are not independent
z-test Numerical
z-test Numrical Continued
Types of t - tests
till now we have studied single population wala t-test only
2-Sample t-test
Independent Samples
- There are 2 t-tests that are used to test differences between the means of two populations
- Application of either of these tests requires that we are reasonably certain that our samples are 1) Independent 2)Taken from two normally distributed population 3) Both of these t-tests can be used when the population variance is unknown
2-Sample t-test
Independent Samples
Test 1
Variance Assumed to be equal
Test 1
Independent Samples
- The population variances are assumed to be equal and the sample observations are pooled
- A pooled variance is used with the t-test for testing the hypothesis that the means of two normally distributed population are equal when the variances of the populations are unknown but assumed to be equal
2-Sample t-test
Independent Samples
Test 1
Variance Assumed to be Equal
Test Statistics
Since we assume that the variances are equal we just add the variances of the two sample means in order to calculate the standard error in the denominator
2-Sample t-test
Independent Samples
Test -2
Variance not assumed to be equal
Test 2
Independent Samples
- No assumption is made regarding the equality between the two population variances and the t-test uses an approximated value for the degrees of freedom
- The t-test for equality of population means when the population are normally distributed and have variances that are unknown and assumed to be unequal uses the sample variances of both populations
2-Sample t-test
Independent Samples
Test -2
Variance not assumed to be equal
Test Statistics
2 Sample t- test
Dependent Samples
- If the observations in two samples both depend on some other factors we can construct a paired comparison test of the means of the differences between observations for two samples are different
- Dependence may result from an event that affects conditions both sets of observations for a number of companies Or because for two firms ?
- Overtime are both influenced by market returns or economic
2 Sample t-test
Dependent Samples
Hypothesis Testing Equation
2 - Sample t-Test
Dependent Samples
Test Statistics
t-Test
Important Note
Chi-Square Test
Definition
- Similar to other hypothesis tests the chi square tests compares the test statistics to a critical chi-square values at a given level of significance and n-1 degrees of freedom :- N-1
What parameter does t-test and z-test involve ?
Means
What parameter does Chi-Square and F-test involve ?
Variance
Chi - Square Test
Properties
- The chi-squared test is used for hypothesis test concerning the variance of a normally distributed population :- V
- Note that since the Chi-Square test is bounded below by zero chi-square values cannot be negative :- N
- The chi square distribution is asymmetrical And approaches the normal distribution in shape as the degrees of freedom increases :- A
Chi-Square Test
Null Hypothesis and Alternate Hypothesis
Chi-Square Test
Test Statistics
Chi-Square
Example
Chi- Square Test
Example Continued
Chi-Square Test
Test Statistics
What is the difference between Chi Square and F Test ?
Chi-Square is used when we are dealing with the variance of the single normally distributed population where as F-test is used when we are dealing with the variance of 2 normally distributed population .
F-Test
Testing the Equality of Variances of Two Normally Distributed Populations
- Based on Two Independent Random Samples is tested with an F-Distributed Test Statistics
Assumption
Population from which samples are drawn are normally distributed
and
that the samples are independent
F-Test
Null and Alternate Hypothesis
F-Test
Test Statistics
Chi-Square Test
F-Test
Parametric Tests
- Parametric Tests rely on the assumptions regarding the distribution of the population and are specific to population parameters
- For Example z-test relies upon a mean and a standard deviation to define the normal distribution
- The z-test also requires that either the sample is large relying on the central limit theorem to assure a normal sampling distribution or that the population is normally distributed
Non Parametric Tests
- Non Parametric Tests either do not consider a particular population parameter or have few assumption about the population that is sampled
- Non parametric tests are used when there is concern about other than the parameters of distribution or the assumptions of parametric tests can’t be supported
- They are also used when data are not suitable for parametric tests (ranked observations )
Non-Parametric Test Cont…
Situations where a non parametric test is called for
- The assumptions about the distribution of the random variable that support a parametric test are not met . An example would be a hypothesis test of the mean value for a variable that comes from a distribution that is normal and is of small size so that neither the t-test nor the z-test are appropiate.
- When data are ranks (an ordinal measurement scale ) rather than value.
- The hypothesis does not involve the parameter of distribution such as testing whether a variable is normally distributed . We can use a non-parametric test called a run test to determine whether data are random . A run test provides an estimate of the probability that a series of changes are random
Spearman Rank Correlation Test
- It can be used when data are not normally distributed
- Consider the performance ranks of 20 mutual funds for 2 years .
- The ranks (1 through 20 ) are not normally distributed so a standard t-test is not appropriate
Spearman Rank Correlation Test
- A large positive value of the Spearman Rank Correlation such as .85 would indicate a high rank in one year if associated with a high rank in second year
- Alternatively a large negative rank correlation would indicate that high rank in year one suggest a low rank in year two and vice versa
