S2. Parameters, Statistics and estimation

Question 1

Define parameter

Answer 1

Numerical measure that describes a specific characteristic.

Question 2

Define statistic

Answer 2

Numerical measure that describes a specific characteristic of a sample

‘Function of a random variable.’

Question 3

Define estimand

Answer 3

The parameter in the population which is to be estimated in a statistical analysis.

Question 4

Define estimator

Answer 4

A function for calculating an estimate of a given population parameter based on randomly sampled data.

Question 5

Define estimate

Answer 5

The numerical value of the estimator given a specific sample is drawn; a non-random number.

Question 6

Notation for population parameters and sample estimators

Answer 6

Question 7

Equations for mean (population parameter and sample estimator)

Answer 7

Question 8

Equations for variance (population parameter and sample estimator)

Answer 8

Question 9

Equations for variance (binary) (population parameter and sample estimator)

Answer 9

Question 10

Equations for standard deviation (population parameter and sample estimator)

Answer 10

Question 11

Equations for covariance (population parameter and sample estimator)

Answer 11

Question 12

Equations for covariance (binary) (population parameter and sample estimator)

Answer 12

Question 13

Equations for correlation (population parameter and sample estimator)

Answer 13

Question 14

Characteristics of an estimator

Answer 14

1. Statistic, hence subject to sampling variation, therefore
2. it has a distribution (with PMF, PDF, CDF) called a ‘sampling distribution.’
3. This sampling distribution has an expected value and variance too.

Question 15

Three properties of a good estimator

Answer 15

1. Unbiasedness
2. Efficiency
3. Consistency

Question 16

Mathematical definition of a bias and an unbiased estimator

Answer 16

Question 17

Mathematical definition for a biased and unbiased estimator

Answer 17

Question 18

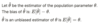
Define standard error

Answer 18

A measure of variation in the sampling distribution of a statistic.

Question 19

Define standard deviation

Answer 19

A measure of variation in data; equal to the square root of variance in the data.

Question 20

Suppose set of iid samples of size N from a population with mean μ and variance σ².

What is the sample mean?

Answer 20

Question 21

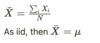
Suppose set of iid samples of size N from a population with mean μ and variance σ².

What is the variance of the sample mean?

Answer 21

Question 22

Suppose set of iid samples of size N from a population with mean μ and variance σ².

What is the standard error?

Answer 22

Question 23

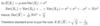
What is meant by consistency? When is an estimator consistent?

Answer 23

If the sequence of estimates can be mathematically shown to converge in probability to the population parameter, it is ‘consistent’, otherwise it is ‘inconsistent.’

Question 24

What happens to sampling distribution with larger sample sizes?

Answer 24

It concentrates and the probability that the estimate is arbitrarily close to the population parameter converges to 1.

Hence why we include N in our calculations.

Question 25

Are consistent estimators unbiased?

Answer 25

Not necessarily. But we can use the fact that:

• the variance of an estimator goes to zero as the sample size grows, and
• the bias goes to zero as the sample size grows.

to establish a sufficient condition for an estimator.

Question 26

Example of a biased, consistent estimator

Answer 26

Variance before Bessel’s correction.

As sample sixe increases, the bias gets smaller and closer to zero, which is enough to make it consistent.