M4. Covariance, Correlation and Independence

Question 1

Define covarience

Answer 1

Cov (X, Y) = E[ (X - E{X}) (Y - E{Y}) ]
Cov (X, Y) = E[XY] - E[X]E[Y]

Question 2

Covariance when x=y

Answer 2

It is just variance.

Question 3

Covariance rules about above/below respective means

Answer 3

If both are the same (both above/below): covariance tends to be positive.

If opposite (one above, other below): covariance tends to be negative.

Question 4

Properties of covariance

Answer 4

Points 4 and 5 link to bilinearity

Question 5

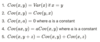
The sum of two variances

Answer 5

Question 6

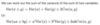
Covariance (and correlation) if x and y are independent

Answer 6

X and Y are independent → E[xy] = E[x]E[y] → Cov(x,y) = E[xy] - E[x]E[y] = 0

Independence implies 0 covariance, 0 covariance implies 0 correlation, but not the inverse.

Question 7

Define correlation

Answer 7

Correlation is just covariance between standardised variables.

Question 8

What is mean independence?

Answer 8

Question 9

4 things to remember about covariance, correlation and independence

Answer 9