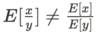M1. Expectations

Question 1

Define expected value (mathematically)

Answer 1

Question 2

What the expected value of a function of a variable?

Answer 2

Question 3

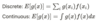
Expected value for:

U(a, b)

N(μ, σ²)

Answer 3

Uniform between {a,b}, so the expected value will be the midpoint i.e. 1/2(a+b).

Normal will have expected value of μ.

Question 4

Operational rules for expected values

Answer 4

Affine functions (useful for when changing units):

E[a+bx] = a + bE(x)

Addition: if h(y) is another function of a variable (another or same) then:

E[g(x)+h(y)] = E[g(x)] + E[h(y)]

E[x+y] = E[x] + E[y]

Multiplication:

E[g(x)h(y)] = E[g(x)] + E[h(y)]

If independent: E[xy] = E[x]E[y]

Question 5

What is Jensen’s inequality?

Answer 5

The expected value of a nonlinear function of a variable is not equal to the nonlinear function of the expected value.

Question 6

Jensen’s inequality for concave functions

Answer 6

E[f(x)] ≤ f(E[x]) if f is concave.

Question 7

Jensen’s inequality for convex functions

Answer 7

E[f(x)] ≥ f(E[x]) if f is convex.

Question 8

Jensen’s inequality for logarithms

Answer 8

Logs are concave so E[log(x)] ≤ log(E[x]).

Question 9

Jensen’s inequality for exponential functions

Answer 9

Exponential functions are convex so e^E[x] ≤ E[e^x]

Question 10

Jensen’s inequality for squaring

Answer 10

Squaring is a convex function so E[x²] ≥ (E[x])²

Question 11

Jensen’s inequality for square roots

Answer 11

Square roots are concave functions so E[√x] ≤ √E[x]

Question 12

Jensen’s inequality for ratios

Answer 12

Ratios of expected values are in general not equal to expected values of ratios.