Polynomials Flashcards
(15 cards)
What are the
steps
to calculating
(4x2y − 3xy + 25) − (9y2 + 7xy − 20)?
-
Distribute −1
(4x2y − 3xy + 25) − 9y2 − 7xy + 20 -
Group like terms
4x2y − 9y2 + xy(−3 − 7) + (25 + 20) -
Simplify
4x2y − 9y2 − 10xy + 45
When
expanding binomials,
how do you
determine the
coefficient of
each term?
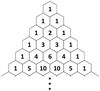
Pascal’s triangle
or
The binomial theorem
or
The “trick”
Besides
Pascal’s triangle and the
binomial theorem,
how can you determine the
coefficients when
expanding binomials?
i.e.
_x7 + _x6y + _x5y2 + _x4y3 + _x3y4 + _x2y5 + _xy6 + _y7
PT = previous term
(x-power of PT) (coefficient of PT)
(index of PT)
What do the
numbers in
Pascal’s triangle
indicate?
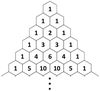
The
- *number** of
- *paths** to
- *each node**.

What is one
real-life example of
Pascal’s triangle
applied to a
binomial distribution?
Coin flips
- H (1)
T (1) - HH (1)
HT TH (2)
TT (1) - HHH (1)
HHT HTH THH (3)
HTT THT TTH (3)
TTT (1) - HHHH (1)
HHHT HHTH HTHH THHH (4)
HHTT HTHT HTTH THHT THTH TTHH (6)
TTTH TTHT THTT HTTT (4)
TTTT (1)
↓

If expanded,
how many
terms will
(3y3 + 6x3)5
have?
Six
An
expanded binomial
will always have
one more term than the
exponent.
What is the
binomial theorem?
x: first term of binomial
a: second term of binomial
n: number of terms
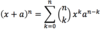
To expand
(ax + by)n,
what three things
do you
need to determine?
-
Number of terms
* (n + 1)* -
Coefficient of each term
* (Pascal’s triangle, the binomial theorem, or the “trick”)* -
Exponents of the variables on each term
* (each will be a natural number and they will add up to n)*
What is the
fundamental theorem of algebra?
Every
non-zero,
single-variable,
degree n polynomial with
complex coefficients has (counted with multiplicity)
exactly n complex roots.
How many roots
does
x2 − 4x + 5
have
Two complex roots
- Per the fundamental theorem of algebra.*
- Here, both are nonreal roots.*
If
one root of
f(x) = x2 − 4x + 5
is
2 + i,
what else do you know?
The
other root is
2 − i

Nonreal roots
always come in
conjugate pairs.
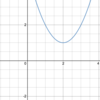
Given the graph of the
fourth-degree polynomial below,
how many
roots will it have?
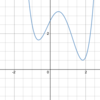
- *Four nonreal roots**
- (in two conjugate pairs)*
How many
real roots might a
third-degree polynomial
have?
One or three real roots
- Must have three complex roots per the fundamental theorem of algebra*
- Must have an even number of nonreal roots because nonreal roots come in conjugate pairs.*
When
dividing a polynomial,
how do you know you’ve
found the
remainder?
When what you have left to divide is a
lower degree than the divisor
Given that
a(x) = −18x2 − 6x + 12
and
b(x) = 3x3 + 9x − 1,
and that
a(x) = q(x) + r(x)
b(x) b(x)
what are q(x) and r(x)?
q(x) = 0
r(x) = −18x2 − 6x + 12
The
quotient is zero, and the
dividend is the remainder because it is of a
lower degree than the divisor


