Complex Numbers Flashcards
What are
- *two other names** for the
- *complex plane**?
z-plane
Argand plane
(a + bi ) (a − bi ) = _____
a2 + b2
&
|a + bi |2
For complex number
z = a + bi,
|z| = _____
√(a2 + b2)
In other words:
√( Re(z)2 + Im(z)2)
Absolute value means
distance from zero, whether the number is real or imaginary.
The absolute value of a complex number can be obtained by applying the Pythagorean theorem.
If you
don’t know the
real part and imaginary part of a
complex number,
what
other information
may allow you to
uniquely describe that number?
Absolute value
&
Angle
(or argument)
(or modulus)
If you
don’t know the
absolute value and angle of a
complex number,
what
other information
may allow you to
uniquely describe that number?
Real part
&
Imaginary part
In complex numbers,
what does
absolute value
refer to?
The
- *absolute value**, or
- *modulus**, gives the
- *distance** of the number from the
- *origin** in the complex plane.
In complex numbers,
what does
angle
refer to?
The
- *angle**, or
- *argument**, is the angle the number forms with the
- *positive real axis**.
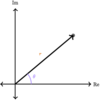
How do you find the
- *angle** of complex number
- a + bi ***?
Θ = _____?
Θ = tan−1 (b/a_)_
- The slope of the line that intersects the number and the origin.*
- Just as with real numbers on a Cartesian plane.*
What are
- *three forms** of a
- *complex number**?
Rectangular form:
a + bi
Polar form:
r (cosΘ + i sinΘ))
Exponential form:
r•e<em>i</em> Θ
What
form is the complex number
2√(3) + 2i
written in?
Rectangular form
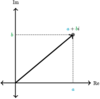
What is the
rectangular form of a
complex number
useful for?
Adding and subtracting
complex numbers.
It’s the sum of two terms: the real part and the imaginary part.
Plotting
in the complex plane.
It gives you the two coordinates.
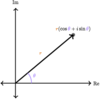
What is the
polar form of a
complex number
useful for?
Multiplying and dividing
complex numbers.
The product of two numbers with absolute values
r1 and r2 and angles Θ1 and Θ2 will have an absolute value r1 • r2 and angle Θ1 + Θ2.
Example:
- z1 has absolute value r1 and angle Θ1.
- z2 has absolute value r2 and angle Θ2.
- z1 • z2 = (r1 • r2) (cos(Θ1 + Θ2) + i sin(Θ1 + Θ2)).
How does the
exponential form of a complex number
relate to the
polar form?
It
uses the same attributes
as polar form (absolute value and angle), but
displays them in a
more compact way.
Example:
- z1 has absolute value r1 and angle Θ1.
- z2 has absolute value r2 and angle Θ2.
- z1 • z2 = (r1 • e<em>i</em> Θ1) • (r2 • e<em>i</em> Θ2) = (r1 • r2) • e<em>i</em> (Θ1+Θ2)
What
form is the complex number
4 (cos (π/6) +i sin (π/6))
written in?
Polar form
What
form is the complex number
4e(π/6)<em>i</em>
written in?
Exponential form
How do you state
- *complex number** z in
- *rectangular form**?
z = _____
z = a + bi
a: real part
b: imaginary part
* i:* imaginary unit
How do you state
- *complex number** z in
- *polar form**?
z = _____
z = r (cosΘ + i sinΘ)
r: absolute value or modulus
Θ: angle or argument
i: imaginary unit
How do you state
- *complex number** z in
- *exponential form**?
z = _____
z = r•e<em>i</em> Θ
r: absolute value or modulus
Θ: angle or argument
i: imaginary unit
In what quadrant of the complex plane does
3 + 4i
lie?
Quadrant I
In what quadrant of the complex plane does
−3 + 4i
lie?
Quadrant II
In what quadrant of the complex plane does
−3 − 4i
lie?
Quadrant III
In what quadrant of the complex plane does
3 − 4i
lie?
Quadrant IV
Why is the
quadrant of a
complex number
important?
Because the calculator may give the
opposite angle,
so you may need to
add 180° or π to the result.
Example:
- −3 + 4i
(located in Quadrant II) - tan−1 (4/−3) ≈ −53°
(located in Quadrant IV) -
Must add 180° to result from calculator to obtain the opposite angle:
−53° + 180° = 127°
How do you restate
z = 4 (cos(π/6) + i sin(π/6))
in
rectangular form?
Expand
the parentheses in the
polar representation.
What are the steps to restating
z = 2√(3) + 2i
in
polar form?
-
Find the angle
Θ = tan−1 (2 / (2√(3)))
Θ = π/6 -
Find the absolute value
r = √( (2√(3))2 + 22)
r = √( 12 + 4)
r = 4 -
Plug in
z = 4 (cos(π/6) + i sin(π/6))
Given complex number z’s
absolute value r
and
angle Θ,
how do you obtain its
rectangular form?
z = r cos(Θ) + r sin(Θ) i
This results from using trigonometry in the right triangle formed by the number and the Real axis.
How do you obtain the
real part of a complex number
given its
absolute value r
and
angle Θ?
r cos(Θ)
This results from using trigonometry in the right triangle formed by the number and the Real axis.
How do you obtain the
imaginary part of a complex number
given its
absolute value r
and
angle Θ?
r sin(Θ)
This results from using trigonometry in the right triangle formed by the number and the Real axis.
Given
z1 = r1 (cosΘ1 + i sinΘ1)
&
z2 = r2 (cosΘ2 + i sinΘ2),
z1 • z2 = _____
z1 • z2 = (r1 • r2) (cos(Θ1 + Θ2) + i sin(Θ1 + Θ2))
Example:
- z1 = 5 (cos 15° + i sin 15°)
z2 = 3 (cos 45° + i sin 45°) - z1 • z2 = (5 • 3) (cos (15° + 45°) + i sin (15° + 45°))
- = 15 (cos 60° + i sin 60°)
Given
z1 = r1 (cosΘ1 + i sinΘ1)
&
z2 = r2 (cosΘ2 + i sinΘ2),
z1 = _____
z2
z1 = (r1 / r2) (cos(Θ1 − Θ2) + i sin(Θ1 − Θ2))
z2
Example:
- z1 = 75 (cos 289° + i sin 289°)
z2 = 25 (cos 83° + i sin 83°) - z1 / z2 = (75 / 25) (cos (289° − 83°) + i sin (289° − 83°))
- = 3 (cos 206° + i sin 206°)
Given
z1 = r1 e<em>i</em> Θ1
&
z2 = r2 e<em>i</em> Θ2,
z1 • z2 = _____
z1 • z2 = (r1 • r2) e<em>i</em> (Θ1 + Θ2)
Example:
- z1 = 9 e<em>i</em> π/4
z2 = 3 e<em>i</em> π/12 - z1 • z2 = r1 e<em>i</em> Θ1 • r2 e<em>i</em> Θ2
- = (r1 • r2) e<em>i</em> (Θ1 + Θ2)
- = (9 • 3) e<em>i</em> (π/4 + π/12)
- = 27 e<em>i</em> (3π/12 + π/12)
- = 27 e<em>i</em> (4π/12)
- = 27 e<em>i</em> π/3
Given
z1 = r1 e<em>i</em> Θ1
&
z2 = r2 e<em>i</em> Θ2,
z1 = _____
z2
z1 / z2 = (r1 / r2) e<em>i</em> (Θ1 − Θ2)
Example:
- z1 = 9 e<em>i</em> π/4
z2 = 3 e<em>i</em> π/12 -
z1 = z1 • z2−1
z2 - = 9 e<em>i</em> π/4 (3 e<em>i</em> π/12)−1
- = 9 (1/3) e<em>i</em> π/4 − <em>i</em> π/12
- = 3 e<em>i</em> (π/4 − π/12)
- = 3 e<em>i</em> (3π/12 − π/12)
- = 3 e<em>i</em> (2π/12)
- = 3 e<em>i</em> π/6
If
- z1 = 1.5 (cos45° + i sin45°),
- z2 = 3 (cos15° + i sin15°), and
- z3 = z1 z2
what will the
- *graph of z3** look like
- *relative to that of z1**?
Scaled by a factor of 3
Rotated by +15° (counterclockwise)
(add angles)
- z3 = z1 z2
- = 1.5 (cos45° + i sin45°) • 3 (cos15° + i sin15°)
- = (1.5 • 3) (cos(45° + 15°) i sin(45° + 15°))
- = 4.5 (cos60° + i sin60°)
(multiply absolute values)
If
- z1 = 5 (cos75° + i sin75°),
- z2 = 2 (cos30° + i sin30°), and
- z3 = z1
z2
what will the
- *graph of z3** look like
- *relative to that of z1**?
Scaled by a factor of 1/2
Rotated by −30° (clockwise)
(subtract angles)
- z3 = z1
z2 - = 5 (cos75° + i sin75°)
2 (cos30° + i sin30°) - = (5/2) (cos(75°−30°) + i sin(75°− 0°))
- = 2.5 (cos45° + i sin45°)
(divide absolute values)
If
z is a complex number,
u is a complex number,
ū is the complex conjugate of u,
and
q = z•u•ū,
then how will the
- *angle of q** appear relative to the
- *angle of z**?
They will have the
same angle.
If the
angle of u is Θ, then the
angle of ū is −Θ.
So the successive multiplications have
no total rotation.
If
z is a complex number,
u is a complex number,
ū is the complex conjugate of u,
and
q = z•u•ū,
then how will the
- *magnitude of q** appear relative to the
- *magnitude of z**?
The magnitude will be
z | u |2.
Both u and ū have the
same absolute value.
So the total effect of mutiplying by u and ū is to stretch everything by a factor of
| u | • | ū | = | u |2.
z = a + bi = _____
u c + di
z • ū
|u|2
-
z = a + bi
u c + di - = a + bi • (c − di )
c + di (c − di ) - = (__a + bi ) (c − di )
c2 + d2 - = z • ū
|u|2
If
z1 is a complex number,
then how will the
- *graph of z1 • i** appear
- *relative to that of z1**?
Rotated +90° about the origin.
Note:
- multiplication by i 2 is a +180° rotation (i 2 = −1)
- multiplication by i 3 is a +270° rotation (i 3 = −i )
- multiplication by i 4 is a +360° rotation (i 4 = 1)
Given
z = r (cosΘ + i sinΘ)
zn = _____
zn = rn (cos(n • Θ) + i sin(n • Θ))
Given
z = 2(cos60° + i sin60°),
what is
- *absolute value** of
- *z3**?
8
|z3| = r3 = 23 = 8
Stretched by a factor of 2 three times, so ultimately stretched by a factor of 23 = 8.
Given
z = 2(cos60° + i sin60°),
what is
- *angle** of
- *z3**?
180°
60° + 60°+ 60° = 3 • 60° = 180°
Rotated by +60° three times, so ultimately rotated by 180°.
Visualize
z = √(2) (cos 45° + i sin 45°)
on the
complex plane.
The plot of
z = √(2) (cos 45° + i sin 45°)
is below.
Disregarding any change affecting the angle,
what would
z4
look like?
The plot of
z = √(2) (cos 45° + i sin 45°)
is below.
Disregarding any change affecting the modulus,
what would
z4
look like?
What are the steps to solving
(−2 + 2√(3) i )3?
-
Find the absolute value
r = √(a2 + b2)
= √((−2)2 + (2√(3))2)
= √(4 + 12)
= 4 -
Find the angle
NOTE: Θ is in Quadrant II
Θ = tan−1 (b/a)
= tan−1 ((2√(3)/−2)
= −60° + 180°
(must add 180° to obtain opposite angle)
= 120° -
Restate in polar form
z = r (cosΘ + i sinΘ)
−2 + 2√(3) i = 4 (cos120° + i sin120°) -
Apply exponentiation
zn = rn (cos(n • Θ) + i sin(n • Θ))
(−2 + 2√(3) i )3 = 43 (cos(120°•3) + i sin(120°•3))
= 64 (cos360° + i sin360°)
= 64 (1) + 64i (0)
= 64
If
z5 = 32,
what are the steps to calculating
z = _____?
-
Restate in polar form
z5 = 32
= r5 (cos5Θ + i sin5Θ) -
Find the absolute value
z5 = 32
r5 = 32
r = (32)^(1/5)
r = 2 -
Find the angle
cos5Θ = 1
5Θ = 0° + 360°k
(must add 360°k to include all possible angles)
Θ = 0° + 72°k
= 72° (where 0° < Θ < 90°) -
Plug in
z = r (cosΘ + i sinΘ)
= 2 (cos72° + i sin72°)
= 2cos72° + 2i sin72°)
≈ 0.618 + 1.902i
