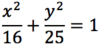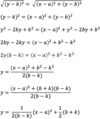Conic Sections Flashcards
Name each
conic section.
Circle
Ellipse
Parabola
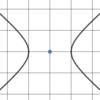
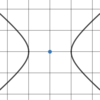
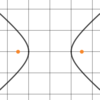
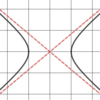
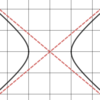
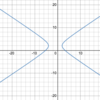
Hyperbola
What
information
do you need to write the
equation of a
circle in standard form?
- Center (h, k)
-
and either
- Radius
- or*
- Another Point on the Circle
What is the
- *standard equation** of a
- *circle**?
(x − h)2 + (y − k)2 = r2
h: x-coordinate of center
k: y-coordinate of center
r: radius length
Given a
circle’s
center at
(−3, 4)
and
radius length of
7,
what is the circle’s
equation in standard form?
(x + 3)2 + (y − 4)2 = 49
Given a
circle’s
center at
(1, 1)
and that
(3, 4)
lies on the circle,
what is the circle’s
radius?
√13
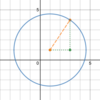
Apply the distance formula
r = √( Δx2 + Δy2)
= √ ((3 − 1)2 + (4 − 1)2)
(it doesn’t matter which point goes first in the subtraction as long as you’re consistent)
= √ ((2)2 + (3)2)
= √ ((2)2 + (3)2)
= √ (4 + 9)
= √13
What is the
- *expanded form** of a
- *circle**?
The result of
expanding the binomial squares
in the standard form and
combining like terms
e.g.:
x2 + y2 − 2x − 4y − 4 = 0
Given this
circle’s equation in
expanded form,
x2 + y2 − 2x − 4y − 4 = 0,
how do you
- *write** the equation in
- *standard form**?
Complete the squares
x2 + y2 − 2x − 4y − 4 = 0
x2 − 2x + y2 − 4y − 4 = 0
x2 − 2x + y2 − 4y = 4
(x2 − 2x + 1) + (y2 − 4y + 4) = 4 + 4 + 1
(you know which numbers to add by halving each of the first-degree terms and then squaring that result)
(x − 1)2 + (y − 2)2 = 9
What is the
- *standard equation** of an
- *ellipse**?
(x − h)2 + (y − k)2 = 1
<span>a</span>2 b2
h: x-coordinate of center
k: y-coordinate of center
a: horizontal radius (think of as rh)
b: vertical radius (think of as rv)
What are the
noteworthy points
of an
ellipse?
Center
Foci
Vertices
Co-vertices
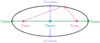
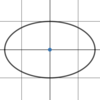
What point is
shown here?
The
- *center** of an
- *ellipse**
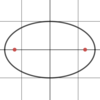
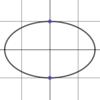
What points are
shown here?
The
- *foci** of an
- *ellipse**
What points are
shown here?
The
- *vertices** of an
- *ellipse**
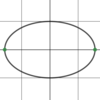
What points are
shown here?
The
- *co-vertices** of an
- *ellipse**
What are the
noteworthy distances
of an
ellipse?
Major radius
Minor radius
(q)
Focal length
(f )
(p)
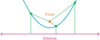
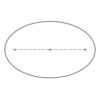
In the
ellipse below,
what
distance is shown?
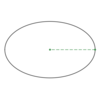
The
major radius
The distance from the
center to
either vertex
Usually called p
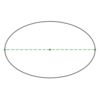
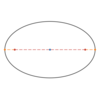
In the
ellipse below,
what
distance is shown?
The
minor radius
The distance from the
center to
either co-vertex
Usually called q
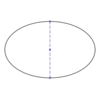
In the
ellipse below,
what
distance is shown?
The
focal length
The distance from the
center to
either focus
Usually called f
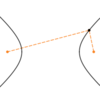
From any
- *point** (N) on an
- *ellipse**, the combined
- *distances** to the
- *foci** (f1 and f2) is equal to what?
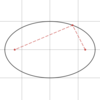
d(N, f1) + d(N, f2) = 2p
- Or two times the length of the major radius*
- How we know this:*
- Vertices (v1 and v2, in orange) each lie along the major axis at a distance of p away from the center, so they are symmetrical about the center
- Foci (f1 and f1, in red) each lie along the major axis at a distance of f away from the center, so they are symmetrical about the center
- Therefore, the red lengths are congruent and the orange lengths are congruent
f = f
p = p - The vertices lie on the ellipse, so by definition, the distance from v1 to f1 plus the distance from v1 to f2 is equal to some constant amount (k):
d (v1, f1) + d (v1, f2) = k -
d (v1, f1) = p − f
d (v1, f2) = 2f + p − f -
k is equal to 2f (the red length) plus 2(p − f ) (the orange amount)
k = 2f + p − f + p − f
= 2p
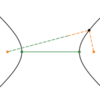
In an
ellipse,
what’s the
relationship between the
major radius, minor radius, and
focal length?
f 2 = p2 − q2
Derived from the
Pythagorean theorem
With any two pieces of information,
you can calculate the third
How we know this:
- d (c1, v1) + d (c1, v2) = 2p
- Co-vertices (c1 and c2) are equidistant from the foci
- d* (c1, v1) = d (c1, v2)
- 2d (c1, v1) = 2p
- d* (c1, v1) = p
- q is purple; f is red; p is orange
- q2 + f 2 = p2
- f *2 = p2 − q2
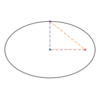
What is the
- *center** of this
- *ellipse**?
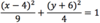
(4, −6)
The standard equation of an ellipse is
(x − h)2 + (y − k)2 = 1
rh2 rv2
where (h, k) is the center of the ellipse, so the coordinates both switch signs
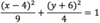
What is the
- *major radius** of this
- *ellipse**?
p = 3
- The major radius, or p, is the longer of the ellipse’s two radii*
- When an ellipse is in standard form, the radius lengths are squared*
What is the
- *minor radius** of this
- *ellipse**?
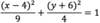
q = 2
- The major radius, or p, is the longer of the ellipse’s two radii*
- When an ellipse is in standard form, the radius lengths are squared*
An
ellipse’s
center is (−1, 1),
major radius is 6,
minor radius is 4, and
vertices are (−1, 7) and (−1, −5).
How would the ellipse be
written in standard form?
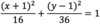
An
ellipse’s
center is (0, 0),
major radius is 5,
minor radius is 4, and
co-vertices are (4, 0) and (−4, 0).
How would the ellipse be
written in standard form?
Graphically,
parabolas can be viewed
as the set of
all points whose
distance from
_____ is
equal to their distance from
_____.
a certain point
and a
certain line
(the directrix)
(the focus)
Given a
parabola’s
focus at (6, −4) and
directrix at y = −7,
how would you write its
equation?
-
Write an equation
distance to focus = distance to directrix
for any point (x, y) on the parabola - Solve for the first-degree term
√((y + 7)2) = √( (x − 6)2 + (y + 4)2)
(y + 7)2 = (x − 6)2 + (y + 4)2
y2 + 14y + 49 = (x − 6)2 + y2 + 8y + 16
14y − 8y = (x − 6)2 + 16 − 49
6y = (x − 6)2 − 33
y = (x − 6)2 − 11
6 2
What is the
- *equation** for the
- *parabola** below in terms of its
- *focus and directrix**?
y = _____
1 • (x − a)2 + 1 • (b + k)
2 (b − k) 2
a: x-coordinate of focus
b: y-coordinate of focus
k: directrix
What are the
- *major features** of
- *hyperbolas**?
- Center
- Vertices
- Foci
- Asymptotes
-
Directions
(open up/down or left/right)
What point is
shown here?
The
- *center** of a
- *hyperbola**
What points are
shown here?
The
- *vertices** of a
- *hyperbola**
What points are
shown here?
The
- *foci** of a
- *hyperbola**
What is
shown here?
The
- *asymptotes** of a
- *hyperbola**
Given hyperbola
(x + 1)2 − (y − 2)2 = 1
9 4
what will its
directions be?
Left/right
Because the x term is positive
Given hyperbola
(y + 1)2 − (x − 2)2 = 1
9 4
what will its
directions be?
Up/down
Because the y term is positive
From any
- *point** (N) on a
- *hyperbola**, the combined
- *distances** to the
- *foci** (f1 and f2) is equal to what?
| d(N, f1) − d(N, f2) | = 2p
Or two times the length from the
center to a
vertex
How do you determine the
- *asymptotes** of a
- *hyperbola**?
Determine
- *what happens** as the
- *negative variable**
- *approaches ±∞**
Example:
y2/4 − x2/9 = 1
y2/4 = x2/9 + 1
y2 = 4/9 • x2 + 4
y = √(4/9 • x2 + 4)
x → ±∞, y ≈ ±√(4/9 • x2)
y ≈ ±√(4/9 • x2)
y ≈ ±2/3 • x (these are the asymptotes)
