Composite Functions Flashcards
(19 cards)
In plainspeak,
and in
one word,
functions are _____.
Maps
They map from
one set of numbers to
another set.

Given functions
g(x) and h(n),
how do you describe
g(h(n))?
A
composite function
Formally,
what is the
definition of a
function composition?
( M ◦ C )(a) = M (C (a))
”( M ◦ C )(a)” is read as
“M composed with C”
◦
is the
composite function symbol
In plainspeak,
what do
composite functions do?
Take the
input of one function
and give the
output of another function

If
g(x) = x3
and
h(n) = 4n − √(n),
what is
(h ◦ g)?
4x3 − √(x3)
Plug in h(n) as the input value of g(x).
Work from the
inside out.
- Can simplify, but is not necessary.*
- Could also be written as h(g(x)).*
If
g(x) = x3
and
h(n) = 4n − √(n),
what is
(g ◦ h)?
(4n − √(n))3
Plug in h(n) as the input value of g(x).
Work from the
inside out.
- Can simplify, but is not necessary.*
- Could also be written as g(h(n)).*
Given:
- For function D
- Input: Speed of the ship, k
- Output: Duration of the cruise, D(k)
- For function S
- Input: Rate of the river current, x
- Output: Speed of the ship, S(x)
In words,
what will
D(S(x)) tell you?
The
duration of the cruise
as a function of
the rate of the river current
What is
h (f(2))?

6

What is
f (h(3))?

−11

Given
f(x) in blue
and
g(x) in orange,
what best approximates
(g ◦ f)(0)?

1
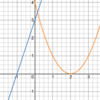
Given
f(x) in blue
and
g(x) in orange,
what best approximates
(f ◦ g)(2)?

3

Formally, if
- *functions f and g** are
- *inverses**, what
- *conditions** must be true?
f (g (x)) = x for all x in the domain of g
g (f (x)) = x for all x in the domain of f
Composing f and g,
in either order,
creates the function that
for every input
returns that input.
Given that
- *f(x) and g(x)** are
- *inverse functions**,
f(g(17)) = _____?
17
For inverse functions f(x) and g(x),
f(g(x)) = x = g(f(x))
f is a
finite function
that is defined by the table below.
Is f an
invertible function?
How do you know?

Yes.
- *Every member** of the domain
- *corresponds** to a
- *unique member** of the range.

h is a
finite function
that is defined by the
mapping diagram below.
Is h an
invertible function?
How do you know?

No.
- *Not every member** of the domain
- *corresponds** to a
- *unique member** of the range.
See diagram below.
h−1 is not a function.

g is a
finite function
that is defined by the table below.
Is g an
invertible function?
How do you know?

No.
- *Not every member** of the domain
- *corresponds** to a
- *unique member** of the range.

y = x3
is
graphed below.
- Is it
a function? - If so, is it
invertible? -
From visual inspection alone,
how do you know
whether it’s invertible?

Yes, it’s a function.
Yes, it’s invertible.
It
passes the horizontal line test.

y = x2
is
graphed below.
- Is it
a function? - If so, is it
invertible? -
From visual inspection alone,
how do you know
whether it’s invertible?

Yes, it’s a function.
No, it’s not invertible.
It’s not invertible because it
fails the horizontal line test.

Given that
f(x) = 2x + 7
and
h(x) = x − 7
2
how do you determine whether f(x) and h(x) are **inverse fuctions**?
Write simplified expressions for
f(h(x)) and h(f(x))
in terms of x.
Example:
STEP ONE:
- f(x) = 2x + 7
- f(h(x)) = 2(h(x)) + 7 (DO NOT SKIP THIS STEP)
- = 2 • x − 7 + 7
2 - = x − 7 + 7
- = x
STEP TWO:
- h(x) = x − 7
2 - h(f(x)) = f(x) − 7 (DO NOT SKIP THIS STEP)
2 - = 2x + 7 − 7
2 - = 2x
2 - = x
f(h(x)) = x = h(f(x))


