Parent Functions

Question 1

Which
parent function
is this?

Answer 1

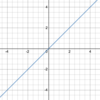
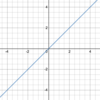
Linear function

Question 2

Which
parent function
is this?

Answer 2

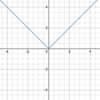
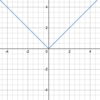
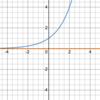
Absolute value function

Question 3

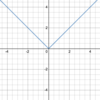
Which
parent function
is this?

Answer 3

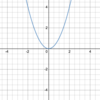
Quadratic function

Question 4

Which
parent function
is this?

Answer 4

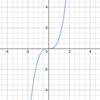
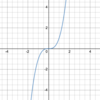
Cubic function

Question 5

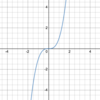
Which
parent function
is this?

Answer 5

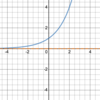
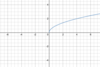
Exponential function

Question 6

Which
parent function
is this?

Answer 6

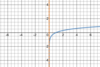
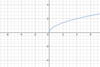
Logarithmic function

Question 7

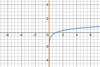
Which
parent function
is this?

Answer 7

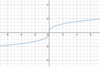
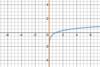
Square root function

Question 8

Which
parent function
is this?

Answer 8

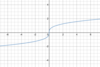
Cube root function

Question 9

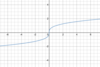
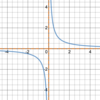
Which
parent function
is this?

Answer 9

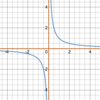
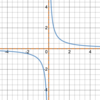
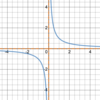
Rational function

Question 10

What family of functions
does

f(x) = −2(x + 3) − 1

belong to?

Answer 10

Linear function family

Degree of one.

Question 11

What family of functions
does

f(x) = −2 | x + 3 | − 1

belong to?

Answer 11

Absolute value family

Absolute value symbols.

Question 12

What family of functions
does

f(x) = −2x² + 3x − 1

belong to?

Answer 12

Quadratic family

Degree of two.

Question 13

What family of functions
does

f(x) = 2^−x + 3

belong to?

Answer 13

Exponential family

Variable in exponent.

Question 14

What family of functions
does

f(x) = −1.5 ln(−x + 4) − 1

belong to?

Answer 14

Logarithmic family

Variable in argument.

Question 15

What family of functions
does

f(x) = −(−x + 2)^1/2 − 2

belong to?

Answer 15

Square root family

Could also be written as
f(x) = −√(−x + 2) − 2

Question 16

What family of functions
does

f(x) = −(−x + 2)^1/3 − 2

belong to?

Answer 16

Cube root family

Question 17

What family of functions
does

f(x) = −2x⁻¹ + 3
belong to?

Answer 17

Rational family

Variable in the denominator.

Could also be written as
f(x) = −2 + 3
x

Question 18

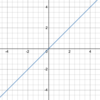
What are the
parent function & general form
of the
linear function?

Answer 18

Parent function:

• *y = x**
• (see below)*

General form:
f(x) = ax + b

Question 19

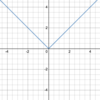
What are the
parent function & general form
of the
absolute value function?

Answer 19

Parent function:

• *y = | x |**
• (see below)*

General form:
f(x) = a | bx + c | + d

Question 20

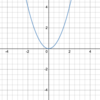
What are the
parent function & general form
of the
quadratic function?

Answer 20

Parent function:

• *y = x^{<span>2</span>}**
• (see below)*

General form:
f(x) = ax² + bx + c

Question 21

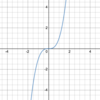
What are the
parent function & general form
of the
cubic function?

Answer 21

Parent function:

• *y = x^{<span>3</span>}**
• (see below)*

General form:
f(x) = ax³ + bx² + cx + d

Question 22

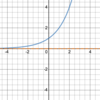
What are the
parent function & general form
of the
exponential function?

Answer 22

Parent function:

• *y = 2^{<span>x</span>}**
• (see below)*

General form:
f(x) = ab^x+c + d

Question 23

What are the
parent function & general form
of the
logarithmic function?

Answer 23

Parent function:

• *y = log x**
• (see below)*

General form:
f(x) = a log (bx + c) + d

Question 24

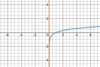
What are the
parent function & general form
of the
square root function?

Answer 24

Parent function:

• *y = √(x)**
• (see below)*

General form:
f(x) = a √(b(x + c)) + d

All
even roots
will look similar.

Question 25

What are the
parent function & general form
of the
cube root function?

Answer 25

Parent function:

• *y = x^1/3**
• (see below)*

General form:
f(x) = a (bx + c)^1/3 + d

All
odd roots
will look similar.

Question 26

What are the
parent function & general form
of the
rational function?

Answer 26

Parent function:
y = 1
x
(see below, a
hyperbola)

General form:
f(x) = a + d
b(x − c)

OR

f(x)
g(x)

OR

f(x) = ax + b
cx +d

Question 27

What are some
noteworthy features
of

f(x) = x?

Answer 27

Domain:
(−∞, ∞)

Range:
(−∞, ∞)

Asymptotes:
None

End behavior:
As x → −∞, f(x) → −∞
As x → ∞, f(x) → ∞​

• x*-intercept:
• *(0, 0)**
• y*-intercept:
• *(0, 0)**

​Other noteworthy points:
​(−1, −1)
(1, 1)

Question 28

What are some
noteworthy features
of

f(x) = | x |?

Answer 28

Domain:
(−∞, ∞)

Range:
[0, ∞)

Asymptotes:
None

End behavior:
As x → −∞, f(x) → ∞
As x → ∞, f(x) → ∞​

• x*-intercept:
• *(0, 0)**
• y*-intercept:
• *(0, 0)**

​Other noteworthy points:
​(−1, 1)
(1, 1)​

Question 29

What are some
noteworthy features
of

f(x) = x²?

Answer 29

Domain:
(−∞, ∞)

Range:
[0, ∞)

Asymptotes:
None

End behavior:
As x → −∞, f(x) → ∞
As x → ∞, f(x) → ∞​

• x*-intercept:
• *(0, 0)**
• y*-intercept:
• *(0, 0)**

​Other noteworthy points:
​(−1, 1)
(1, 1)

Question 30

What are some
noteworthy features
of

f(x) = x³?

Answer 30

Domain:
(−∞, ∞)

Range:
(−∞, ∞)

Asymptotes:
None

End behavior:
As x → −∞, f(x) → −∞
As x → ∞, f(x) → ∞​

• x*-intercept:
• *(0, 0)**
• y*-intercept:
• *(0, 0)**

​Other noteworthy points:
​(−1, −1)
(1, 1)

Question 31

What are some
noteworthy features
of

f(x) = 2^x?

Answer 31

Domain:
(−∞, ∞)

Range:
(0, ∞)

Asymptotes:
Horizontal asymptote:
y = 0

End behavior:
As x → −∞, f(x) → 0
As x → ∞, f(x) → ∞​

• x*-intercept:
• *None**
• y*-intercept:
• *(0, 1)**

Other noteworthy points:
​(−1, 1/2)
(1, 2)
(2, 4)

Question 32

What are some
noteworthy features
of

f(x) = log x?

Answer 32

Domain:
(0, ∞)

Range:
(−∞, ∞)

Asymptotes:
Vertical asymptote:
x = 0

End behavior:
As x → 0, f(x) → −∞
As x → ∞, f(x) → ∞​

• x*-intercept:
• *(1, 0)**
• y*-intercept:
• *None**

Other noteworthy points:
(10, 1)
or:
(BASE, 1)

Question 33

What are some
noteworthy features
of

f(x) = √(x)?

Answer 33

Domain:
(0, ∞)

Range:
(0, ∞)

Asymptotes:
None

End behavior:
As x → 0, f(x) → 0
As x → ∞, f(x) → ∞​

• x*-intercept:
• *(0, 0)**
• y*-intercept:
• *(0, 0)**

Other noteworthy points:
(1, 1)
(4, 2)

Question 34

What are some
noteworthy features
of

f(x) = x^1/3?

Answer 34

Domain:
(−∞, ∞)

Range:
(−∞, ∞)

Asymptotes:
None

End behavior:
As x → −∞, f(x) → −∞
As x → ∞, f(x) → ∞​

• x*-intercept:
• *(0, 0)**
• y*-intercept:
• *(0, 0)**

Other noteworthy points:
(−1, −1)
(1, 1)​

Question 35

What are some
noteworthy features
of

• *f(x) = 1**?
• *x**

Answer 35

Domain:
(−∞, ∞), x ≠ 0

Range:
(−∞, ∞), y ≠ 0

Asymptotes:
Horizontal:
y = 0
Vertical:
x = 0

End behavior:
As x → −∞, f(x) → 0⁻
As x → ∞, f(x) → 0⁺​
As x → 0⁻, f(x) → −∞
As x → 0⁺, f(x) → ∞​

• x*-intercept:
• *None**
• y*-intercept:
• *None**

Other noteworthy points:

• *(−1, −1)**
• *(1, 1)**