Policy Evaluation

Question 1

Identifying assumptions - RCT

Answer 1

• treatment and control groups are on average the same
• on observable and unobservable characteristics; SUTVA

Question 2

Identifying assumptions - regression

Answer 2

• treatment is as good as randomly assigned conditional on observables (CIA)

Question 3

Identifying assumptions - IV, RD

Answer 3

• relevance; independence; exclusion

Question 4

identifying assumptions - DiD

Answer 4

• common trends; no compositional changes; homogenous treatment effect
• Two identifying assumptions for DiD:
  
  • No compositional changes between two groups: e.g. in the minimum wage example if some restaurants go bankrupt, then left with surviving restaurants
  • Common trend, i.e. time effects between groups are the same; cannot prove it, have to assume
    
    • What you can look into is how similar trends of two groups were before time 0; if they are similar, indicates that they might be similar in observed period, but cannot prove since we never observe red line in graph on p. 5
• Be cautious of level vs. log: if common trend in levels, no common trend in logs unless they are the same line (look into this more)

Question 5

identifying assumptions - bounds

Answer 5

• monotone treatment response; monotone treatment selection; monotone instrumental variable

Question 6

stable unit treatment value assumption (SUTVA)

Answer 6

• definition: The potential outcomes for any unit do not vary with the treatments assigned to other units, and, for each unit, there are no different forms or versions of each treatment level, which lead to different potential outcomes. SUTVA requires that the response of a particular unit depends only on the treatment to which he himself was assigned, not the treatments of others around him.
• example: would be violated for treatments of inectious diseases as my outcome (disease or not) depends on treatment of others (if lots treated, less likely to get disease)
• No interference. Often not credible in classroom/school setting; therefore randomize at level of schools classes/schools instead of students
  
  • If maybe spillover between units in different treatment groups, can change their unit of analysis. Students assigned to tutoring program might interact with other students in their school who were not assigned to the tutoring program and influence their grades. To enable causal inference, the analysis might be completed at the school level rather than the individual level. SUTVA would then require no interference across schools, a more plausible assumption than no interference across students. However, generally entails a sharp reduction in sample size. Also changes question that we can answer: no longer learn about the performance of individual students, but of schools.
• No hidden variations of treatments. For example: it shouldn’t matter whether treatment was assigned or chosen

Question 7

Randomized trials - advantages

Answer 7

• Random assignment ) D_i is independent from characteristics of participants
  
  • justifies OLS without control variables (i.e. E (u_i|D_i) = 0)
• Randomization can be based on (pre-treatment) covariates X_i
  
  • justifies OLS with control variables X_i (i.e. E (u_i|D_i, X_i) = E (u_i|X_i))
• Multiple treatment groups/levels of D_i are possible

Question 8

Randomized trials - statistical inference and power

Answer 8

• We never observe the underlying truth, only the data from our sample
• Four possible cases:
  
  • False positive: we find a statistically significant effect even though the true effect is zero (Type I error)
  • True zero: we fail to reject H₀ and there truly is no effect
  • False zero: we fail to reject H₀ even though the true effect is not zero (Type II error)
  • True positive: reject H0 and there truly is an effect. This is the power, the probability that we will not make a type II error: (1 􀀀 )
    
    • power is typically set at 0.8 or 0.9

Question 9

Randomized trials - determinants of power

Answer 9

• likely not on exam
• Effect size
  
  • what chance of finding a statistically significant effect if the true effect size is beta*?
  • given n, what is minimum level of true effect at which we have enough power to reject H₀?
• Residual variance
  
  • including control variables (past outcomes) often reduces residual variance - the width of the bell curves
• Sample size
  
  • also affects the width of bell curves
• Statistical significance
  
  • increasing (from say 5% to 10%) increases the power
• Allocation ratio
  
  • fraction of sample that is assigned to treatment
• Clustering
  
  • individuals versus schools/classes as unit of randomization

Question 10

Minimum detectable effect size

Answer 10

likely not on exam

Question 11

What we need for a power calculation

Answer 11

• likely not on exam
• Desired power: 80 percent, 90 percent …
• MDE size: hardest part, matter of judgement; not a goal or prediction
  
  • using “standard” effect sizes based on a large number of experiments on education; 0.2 is small but respectable, 0.4 is large
  • compare various MDE sizes to those of interventions with similar objectives (aiming at same outcome)
  • what effect size would make the program cost-effective?
• Number of clusters: if cost is not an issue, maximize J, otherwise balance J and g relative to the costs
• Allocation fractions: p_T/p_C = squareroot(c_c/c_t) (assumes given budget for program+evaluation; c per person cost)
• Estimate of the residual variance (historical data, pilot)
• Estimate of the intracluster correlation (historical data, pilot)

Question 12

how a small portion of false positives can be very misleading

Answer 12

• Of hypotheses interesting enough to test, perhaps one in ten will be true. So imagine tests on 1,000 hypotheses, 100 of which are true.
• The tests have a false positive rate of 5%. That means they produce 45 false positives (5% of 900). They have a power of 0.8, so they confirm only 80 of the true hypotheses, producing 20 false negatives.
• Not knowing what is false and what is not, the reseacher sees 125 hypotheses as true, 45 of which are not. The negative results are much more reliable–but less likely to be published.

Question 13

three types of peer effects

Answer 13

• Endogenous interactions
  
  • direct effect from behavior of others on own behavior
• Contextual interactions
  
  • the exogenous characteristics of others affect ones’ behavior
• Correlated effects
  
  • shared environment or characteristics which are unobserved
• why make these distinctions? Separate peer effects (endogenous/contextual interactions) from confounders (correlated effects); implications for spillovers:
  
  • Example: suppose we do extra tutoring
    
    • with endogenous effects other students will indirectly benefit
    • not the case with contextual interactions and/or correlated effects

Question 14

three problems with identifying peer effects

Answer 14

• The reflection/simultaneity problem:
  
  • Do peers affect respondent, or does respondent affect peers?
• The self-selection problem:
  
  • Peers (including respondents) select themselves on similar characteristics
• The correlated unobservables problem
  
  • Are effects driven by behavior or by unobserved characteristics that are correlated with it.
  • It is not always clear how to define a peer group.

Question 15

Randomized trials 1 - Duflo, Dupas, Kremer: Peer effects, teacher incentives, and the impact of tracking: Evidence from a randomized evaluation in Kenya

Answer 15

Experiment

• Randomized experiment in Kenya
  
  • 121 primary schools with one 1st grade class, extra teacher for 2 sections
• Two random treatments
  
  • 60 schools split group randomly in two
  • 61 schools track by first term grades
• Estimate average effect of tracking
• Estimate effect of tracking for the median student

Results

• Tracking is beneficial for students above the median
• Tracking is beneficial for students below the median
• For the median student, it doesn’t matter whether s/he is placed in the upper or the lower track
• What type of production technology and incentive structure could generate these results?
  
  • Linear-in-means (+) can only explain 1, not 2 and 3
  • Linear-in-means (+) and linear-in-spread (–) can explain 1 and 2, but not 3.

Issues

• results violate linear-in-means model
  
  • both students at bottom and top get higher scores with tracking - would only expect that for students in class with lower ppers
  • at middle, continuous, i.e. doesn’t matter if average and placed in higher vs lower groups
    
    • lack of difference might be explained by role of teacher - they focus on better-performing students and base level of study on higher students, so for avg student in to group leve of study is much further from their ability than for below average guy who is in power group and there is a high performer

Question 16

Randomized trials 2 - Miguel, Edward and Kremer: Worms: identifying impacts on education and health in the presence of treatment externalities

Answer 16

• Results only become insignficant if you do three out of four things at the same time (blogs by Blattman and Ozler):
  
  • divide data into two smaller samples (year 1 and year 2)
  • ignore spillovers
  • average outcomes at the school level
  • redefine treatment periods to match calendar years
• ATE seemed low, so thought pills were ineffective, but that was mostly due to externalities–>get people not treated benefitted from treatment of others

Question 17

Regression - OVB

Answer 17

Question 18

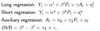
Regression - good vs bad controls

Answer 18

• Some variables are bad controls and should not be included in a regression model even if inclusion changes the coefficient of interest
• Bad controls are variables that are themselves outcome variables
• Good controls are variables that have been fixed at the time the regressor of interest was determined
• Example: Suppose we are interested in the effects of a college degree on earnings and that people can work in one of two occupations, white collar and blue collar
  
  • A college degree clearly opens the door to higher-paying white collar jobs. Should occupation therefore be seen as an omitted variable in a regression of wages on schooling?
  • Lets look at the effect of college on wages for those within an occupation, say white collar only
  • The problem is that if college affects occupation, comparisons of wages by college degree status within an occupation are no longer apples-to-apples, even if college degree completion is randomly assigned
  • Bad control means that a comparison of earnings conditional on occupation does not have a causal interpretation

Question 19

quantile regression

Answer 19

left out, check if necessary

Question 20

IV - reasons to use IV

Answer 20

use if cov(u,x)/=0, i.e. endogeneity

Question 21

IV - how it works

Answer 21

• We want to split x into two parts:
• part that is correlated with the error term (causing E[u_i|x_i]/=0)
• part that is uncorrelated with the error term
• In order to isolate the second part use a variable z with the following properties:
  
  • exogeneity
  • relevance

Question 22

IV - one endogeneous regressor, one instrument

Answer 22

Question 23

IV - reduced form

Answer 23

follows from substituting FS into structural equation

Question 24

IV - Wald estimator (one endogenous regressor, one instrument)

Answer 24

• Wald estimator is IV estimate (transparent version of it)
  
  • E(Y|Z=1) – E(Y|Z=0) (Z is the instrument) – this is the reduced form – divided by E(X|Z=1)-E(X|Z=0) (which is the FS)

Question 25

IV - insutrment exogeneity and Hausman test

Answer 25

• for IV relevance, can simply take F-stat of FS coeffcient of Z on X; rule of thumb: F>10

Question 26

IV - overidentifying restrictions test

Answer 26

• exam question!
• Overidentification restriction test: assuming you have multiple instruments, testing that IV estimate that we get is the same for one instrument as for the other or for any combination of the instruments; so basically testing if on instrument is valid given (assuming) that the other instrument is valid
• exam question: should be able to explain in exam why this is nonsense (i.e. look up why overidentification restriction test is not accurate, working etc.)
  
  • One problem: strong assumption that one is valid
  • Answer has to do with Wald estimate / IV: add a 1 to Z in Wald estimator (i.e. Z₁); if for Z₁ have certain LATE estimate, no reason to assume that instruments effect the exact same groups in exactly the same way (only if that was the case would the Wald estimates be the same? This in parentheses is my addition, so check); only makes sense if we believe in homogeneous treatment effects

Question 27

IV - monotonicity assumption in heterogeneous effects setup

Answer 27

• all those affected by the instrument are affected in the same way
• If monotonicity assumption violated very problematic; e.g. have FS of 0.3, assume this is share of compliers, but if have defiers, could be 0.31-0.01 (would not be that problematic), but if 0.6-0.3 then problematic
  
  • Arguments for why monotonicity should hold in papers: small number of defiers
• in example of the effect of military service on earnings (Angrist, 1990):
  
  • Monotonicity implies that there is no one who would have served in military if given a high lottery number, but not if given a low lottery number
  • Assumption would be violated if someone, who would have volunteered for the Navy when not at risk of being drafted (high lottery number), would have chosen to avoid military service altogether when at risk of being drafted (low lottery number)

Question 28

IV - LATE

Answer 28

• RF is same as ITT, IV estimator is LATE (local means for compliers)
  
  • LATE allows for heterogeneous effects (ITT/ATE not? Check)
• LATE = ITT/FS
• four groups
  
  • Compliers: Xi (1) = 1 and Xi (0) = 0; men who serve if draft eligible, but who don’t serve if draft ineligible.
  • Always-takers: Xi (1) = 1 and Xi (0) = 1; men who always serve in military, regardless of their eligible status
  • Never-takers: Xi (1) = 0 and Xi (0) = 0; men who never serve in military, regardless of their eligible status
  • Defiers: Xi (1) = 0 and Xi (0) = 1; men who don’t serve if draft eligible, but who serve if draft ineligible.
• Who are the compliers?
  
  • With heterogeneous effects IV-estimator is estimate of average causal effect for compliers
  • Different valid instruments for same causal relation therefore estimate different things (different groups of compliers)
  • Overidentifying restrictions test (Sargan test) might reject even though all instruments are valid.
  • We can’t identify the compliers because we can never observe both Xi (0) and Xi (1)
  • those with Zi = 1 and Xi = 1 can be compliers or always-takers
  • those with Zi = 0 and Xi = 0 can be compliers or never-takers
  • We can identify proportion of compliers in population : P(X_i(1) = 1 &X_i(0) = 0) = E[X_i|Z_i=1]-E[X_i|Z_i=0] (firststage)
  • We can get some information about characteristics of compliers by looking at how first stage differs by values of covariates
  • For example: relative likelihood that a complier is a college graduate is ratio of first stage for college graduates to overall first stage
  • In addition if there are no always-takers IV-estimator estimates average treatment effect for the treated
  • And if there are no never-takers IV-estimator estimates average treatment effect for the non-treated

Question 29

RD design

Answer 29

• Outcome Y, variable of interest D (assume binary 0,1), running (forcing) variable W, cutoff w0
• Sharp RD
  
  • Forcing variable W fully determines D with discrete jump at w0
  • Analysis by OLS including W
• Fuzzy RD
  
  • Forcing variable W partly determines D with discrete jump in Prob (D = 1|W) at w0
  • Analysis by IV
• How does bandwidth selection work? If your results depend on what bandwidth you choose, usually not good indication; so want to try out various bandwidths to see if results hold
  
  • Bandwidth: tradeoff between less precise estimates (if include more) and inclusion of more datapoint (more Aussagekraft)
• Donut in RD: if there is a lot of data at the cutoff, don’t include it

Question 30

RD - sharp RD

Answer 30

Question 31

RD - fuzzy RD

Answer 31

Question 32

RD - interpretation

Answer 32

Question 33

RD - bunching at cutoff

Answer 33

• Schools manipulate student numbers to remain below threshold and those that do so are different from other schools

Question 34

Randomized trials 3 - Jayachandran, Laat, Lambin, Stanton: Cash For Carbon: A Randomized Controlled Trial Of Payments For Ecosystem Services To Reduce Deforestation

Question 35

Randomized trials 4 - Ashraf, Berry, Shapiro: Can Higher Prices Stimulate Product Use? Evidence from a Field Experiment in Zambia

Question 36

Regression 1 - Dale, Krueger: Estimating The Payoff To Attending A More Selective College: An Application Of Selection On Observables And Unobservables

Answer 36

• do not have uemplyoed peopel in tsamepl, might be correlated with less
• compare college selection
• match applicant model: selectivity of college on earnings
• problem: unobservable characteristics
• match application: used for being acepted or rejected
  
  • people know their potential, so according to that apply to school
• two biggest issues
  
  • unobservable: ability
  • bad control bgigest issue: retrict sample to employed, but unemplyeod would be related to going to selective / nonselective school)
• Previous literature mostly relies on using OLS with additional regressors to control for ability
  
  • Admission decisions are also based on unobservable characteristics
• Unobserved characteristics are visible for the admissions committee but not for the
  researcher (e.g. motivation letter, college admissions essay, interview)

Question 37

Regression 2 - Leuven, Oosterbeek: An Alternative Approach To Estimate The Wage Returns To Private-Sector Training

Answer 37

• effect of training on earnings
• they had purely random things (people wanted training, but couldn’t for random reason) since usually enogeneity since only people atttend / choose training because are interested
• mean regression more sensitive to outliers
• two ways to deal with endogeneity
  
  • IV: very hard to find proper instrument
  • fixed effects: have time variables, so can’t use fixed effects (e.g. if you buy new equipment has effect), so effects would be overestimated; fixed effects don’t capture time effects (training akes people more likely to attend training)
  • quantile regression: check
    
    • look for median regression: if results are simiar to mean regression, than outliers less likely since median less likely to outliers
  • makes results very robust that these quantile regressions comfirm each other

Question 38

Regression 3 - Dinardo, Pischke: The Returns To Computer Use Revisited: Have Pencils Changed The Wage Structure Too?

Answer 38

Background

• The paper looks at the wage returns associated with different worker
  ‘tools’
• Established that Germany and the US are similar enough to make a useful comparison
• Ran an OLS regression with the tools entered separately
• Controlled for occupation
• Controlled for correlation between use of tools
• Controlled for unobserved heterogeneity
• Still, there is a positive, significant coefficient for the returns to computer use
• Reasons for differential
  
  • Computer users possess unobserved skills that are little to do with
  • computer use but are rewarded in the labour market
  • The introduction of computers changes the wage structure without
  • generating a computer treatment effect
  • The results are suggestive, and do not prove whether the computer
  • coefficients represent a return to skills or a selection effect

Issues

• controlled for typical occupation controls (level of education, gender, age): same controls for other occuptaions may not apply since computer skills are so new
• why no fixed effects: return on computer skills would change over time
• paper showing that there is huge selection effect
• everyone can use pencil, computer skills are limited, still find such large effects (can’t believe computer has effect if pencil has effect?)
• main point: assume that adding controls on unobsrvales would be good, but maybe didn’t control for skills of people using computers
• typical controls might not have been goo controls for learning computer since computer is such new skill
• The coefficients for other tools that
  aren’t scarce as computers, are
  significantly different from zero in all
  the regressions. There is no evidence to support that the laege measures wage differential for on-the-job computer users is a true return to computer skills
• Use of a pencil has a 13% wage differential, seems high?
• Ability to use a pencil not a scarce resource, therefore, there must be some selection bias
• If this selection is important for pencil use, it must be equally important for computer use too
• These results suggest that we can’t wholly attribute the wage differential to a return to computer skills

Question 39

Regression 4 - Oster: Unobservable selection and coefficient stability: Theory and evidence

Question 40

IV 1 - Bhuller et al. Incarceration, Recidivism, and Employment

Answer 40

Background

• Research question: What is the effect of incarceration on recidivism? What is the effect of incarceration on employment?
• Method: IV (judges leniency (either strict of nonstrict)
• Results
  
  • Incarceration ….
  • Decreases recidivism if previously non-employed
  • Increases employment if previously non-employed

Issues

• Defiers in judge case: monotonicity assumption here: every case that is judged by the lenient judge will also be judged by the strict judge (or other way around: for each case not sentenced by the strict judge will not be sentenced by lenient judge)– very strong assumption
  
  • Generally, both ways have to be true – other example doctor: if win lottery, don’t go to med school, but if don’t win, still go – very unlikely
  • this can’t hold since there might be some judges that are particularly strict on specific topics
• never-takers and always-takers: when calculating Wald estimator, eliminate always-takers
  
  • FS is share of compliers (bottom of Wald)
  • top is reduced form
• independence: assures that always-and never takers are same share in table with 4 quadrants
• who are the compliers in the paper?
• exclusion (or monotonicity): assuming that stringency of judge doesn’t depend on case (e.g. lenient, but stringent on sexual assault)

Question 41

IV 2 - de Ree et al. Double for Nothing? Experimental Evidence on an Unconditional Teacher Salary Increase in Indonesia

Answer 41

• spillover minimized since no public announcement
• IV cofirmed ITT estimates
• ITT is more precise, but has more assumptions, so fact that IV confirms ITT shows robustness of results
• ITT: effect of being in treated school on test scores
• IV: effect of being taught by certified teacher
• Argument against performance-based pay - exposes teachers to risks since in small classes, could get lucky and have high-performing students or unlucky and have bad-performing students (i.e. outliers have larger impact at smaller classes); need to compensate teachers for this risk

Question 42

IV 3 - Lundborg et al: Can Women have Children and a Career? IV evidence form IVF Treatment

Answer 42

Background

• Research question: What is the labor market response to having children at the extensive margin?
  
  • extensive fertility margin: labor market effects of having the first child
  • intensive fertility margin: labor market effects of having additional children among women who already have a child/children
• Instrument: success at their first IVF
  treatment, X-varaible is fertility (1 if have children)
• When children are young, women earn less because they work less. When children are older women earn less because they get lower wages.
• results
  
  • Fertility effects are much stronger at the extensive margin than at the intensive margin.
  • Having children hurts women’s careers. The fertility effects at the extensive margin are negative, large, and long-lasting.
  • A second born at the intensive margin has negative effects on earnings in the short run and in the long run the negative fertility effects fade out and dissapear.

Issues

• IV (specify what this is) could affect dependent variable through depression, so exogeneity could be violated
• violation: women how get to 4th stage of IV, then hwo fails or succeeds, women are similar except from age (violation; but they condition on age, so then ok
• OVB
  
  • Health is related to labor market outcomes (Y variable), that’s why relevant to discuss
  • Interested in effects of cause, not causes of an effect (i.e. not explaining fertility or labor market outcomes, but want to explain cause)
    
    • That’s why we don’t look at R², because we’re not interested in predicting labor market outcome, but interested in one particular effect (one beta in regression)
• see table: With this data, coefficient of IVF success on fertility (FS) should be 1; as we progress in years, (0,0) gets smaller and (0,1) (fertility=1) gets larger, so first stage gets smaller (meaning difference between coefficient for (0,0) and (0,1) gets smaller over time)
  
  • Z is randomly distributed, so 0.5 that NT end up in cell 1 or 3, so can calculate NT; also know total number of compliers and share of compliers (compliers/total # of participants); we could not do these calculations if we had defiers as well
  • FS shows share of compliers (look at bottom of Wald estimator)
  • Women who get pregnant have children with different ages, this affects labor market outcome so exclusion assumption will fail
  • Since age of children matters for if women work or no; it also means that women in (0,0) group have older children, so exclusion restriction is violated here
  • IVF success does not only affect probability of having first, but also of having a second child since you can get twins; thus, this does not only affect the extensive, but also the intensive margin
  • So exclusion restriction violated through age of children and number of children
  • In the control group, you now have younger children (worse for control group outcome); also have more children in treatment(?) group, so overestimates effect on extensive margin
• IVF women have children in beginning, then income drops and stays a bit lower the first few years
  
  • some women have children later, so then effect is overestimated (since some of the women in control group have children later,
• being given treatment affects other things that also affect labor market outcome (through age of first child, so exclusion retriction violated, and probability of having second child (could have twins), which also affects labor market outcomes)
• overestimated means negaitve impact of treatment is exaggerated
• health influence on instrument, also other way around (Table 2 columns 8 and 9) - not significant, not problems
• External validity issues
  
  • The women who enter IVF treatment are different from a larger population of
    representative women. They are better educated, work more, earn high salaries, have
    explicit demand for children and are older when they have children.

Question 43

IV 4 - de Mel et al: Returns To Capital In Microenterprises: Evidence From A Field Experiment

Answer 43

Set-up

• ganve random grants to see if they would increase capital, 2nd stage is capital on profits
• four treatments: cash and equipment
• Research Question: What is the effect of positive shocks to the capital stock on the average return on capital of microenterprises?

Issues

• violation to SUTVA due to spillover in bamboo industry; Local spillovers seem to affect real profits: negative spillover effect from within 500 meter treated firms
• exclusion restriction violated since treatment also effects profits through hours worked (Table 2)
  • Real profits in that table is reduced form, so that divided by column 1 is IV estimate
  • Address this issue in columns he didn’t show in presentation that are in table 2
  • adjust for profits to account for labor hours, but bad control
  • ZàKàProfits, but also ZàLàP
  • Solution: control for labor by adding to regression, but that’d introduce bad control variable
    
    • What you do: adjust profit for labor, so do Profit-bL = aK
      
      • b is chosen, so depends on b (i.e. how they value the labor)
    • Through Stata regression could see that first line has higher bias than 3^rd (what does that mean?)
• 2^nd issue: lambda is enterprise-level fixed effects – isn’t there than perfect correlation? (why?); not an issue because they use same firms with treatment and control (we observe treatment people without treatment at baseline, that’s why)
  
  • Make sure to understand why fixed effects here make control group unnecessary
• Third issue: inconsistency in profit column in table 2; does not make sense that if you double treatment you only get half the effect
  
  • See how they deal with this
• they give money prizes to control group to keep attrition low - could compromise results
• local spillover in bamboo industry
• external validity - might take less risky investments if had to pay back (here don’t do that)

Question 44

RD 1 - Angrist, Lavy: Using Maimonides’ Rule To Estimate The Effect Of Class Size On Scholastic Achievement

Answer 44

Other notes

• Predicted class important because use this to explain randomization at discontinuity: idea that students close to discontinuity are assigned predicted class size as good as random, but actual class size might be different; however, show in paper that predicted class size and actual class size are closely related
• Only interested in exogeneous variation in class size (according to Eudenides rule) and ignore endogenous variation­­
• Can use enrolment as explanatory variable because exclusion restriction does not apply to enrolment, but some function of enrolment
• Fuzzy design: schools are deviating from “rule”
  
  • Example of sharp design: if<50% of votes, not elected, <50% elected
• Limits of discontinuity sample (i.e. on each side of threshold)
  
  • Question is how much better do we predict the points at the discontinuity by enlarging the limits
  • On the other hand, data far off the discontinuity point could be weaker at predicting points close to threshold (e.g. classes at 20 students could be very different than classes at 39), so there is a trade-off between enlarging or making the limits smaller

Issues

• Problem: bunching at cut-off shows that independence doesn’t hold (somehow there are school districts that don’t open extra class by admitting new student)
  
  • bunching might be corelated with quality fo schools, e.g. poorer schools who cannot afford additinal teacher imght send students away to remain just below cutoff
• Balancing around cut-off: again, violation of independence – schools just below cut-off have lower household income than just above threshold
• heterogeneity of effects - higher effect for lower incomes
• There is bunching in this paper
• RD advantage: don’t need control group, but find random variable (here student enrollment) and find discontinuity (in that sense differs from RCT)
• weird that different effect for 4th and 5th graders (they said due to cumulative effect, i.e. 5th graders were in 4th grade before, now in 5th) - strong assumption
• use discontinutity as IV, so no endogeneity in discontinuity sample, but still endogeneity in full sample, so probably hard to generalize results
• have different cutoffs since larger schools might be richer

Question 45

RD 2 - Almond, Doyle, Kowalski, Williams: Estimating Marginal Returns To Medical Care: Evidence From At-Risk Newborns

Answer 45

Issues

• Problem with reporting unit since some hospitals report in 100s of grams, some in ounces and some in grams; have to be very cautious that not more hospitals of one category fall on either side of the threshold
  
  • That’s why this paper introduces the donut: exclude 1500g babies; could also make 3 donut, so exclude 1499, 1500, 1501 etc.
  • Paper for donut by barreca, guildi, lindo waddell 2011
  • Whether a hospital reports in grams or ounces can thus point toward the sophistication of the hospital; the “donut paper” finds that the effects of the regression are 0, so probably the effects come from the hospitals and not from whether a baby is below or above the threshold
• Could possibly do analysis only on hospitals that report in 1 grams; this would probably be an issue for external validity
• donuting has effect on measurement error

Question 46

RD 3 - Clark, Martorell: The Signaling Value of a High School Diploma

Answer 46

• point of paper to distinghsh between signalling efect and human capital effect
• barely passers and barely failures are pretty much the same

Issues

• As M&C explain, employers rarely verify high school diplomas; they basically just take applicants’ word for it
• endogeneity / the reason the authors picked exam at end of 12^th grade: Students take exit exams in Texas for the first time in 10th grade and can retake the exams several times before the 10th and 12th grade. The scores on the 10th grade exit exams are endogenous as the scores could influence the length of schooling or the curriculum in later years. As a result, Clark and Martorell (2014) focused on a small proportion (4.83%) of students that took exit exams at the end of 12th grade.
  
  • Students at first exam still have change of failing, retaking and still getting a high school diploma; would have weak first stage as many would go on to 2^nd attempt and still pass
  • Would have very small first stage if we just used passing the first one
• Clark and Martorell (2014) focused on a small proportion (4.83%) of students that took exit exams at the end of 12th grade: These students have already failed the exam at least once, and often several times. Moreover, they have a lower socioeconomic status than students who took exit exams only once (Clark and Martorell 2014). Therefore, the results in this study are unlikely to hold for the majority of the population.
  
  • Maybe this fits here: these students might also apply for jobs that don’t value high school diplomas much anyways
• When discussing independence, not only mention students being similar, but also that students can’t choose where they fall over the threshold
• Study doesn’t account for self-employed people (but maybe have to signal to clients or investors)
• We can’t just look at employed people because that would introduce bad control problem as we would condition on an outcome (you’re then looking at people who even without diploma find a job OR you could see it as the more qualified people go to college, i.e. are unemployed and thus excluded from the sample)
• Exam question: cheaper (rather easier) for more productive people to get diploma
  
  • He’ll inform us about paper inspired by this one (tries to do sth similar in Netherlands – you have seen this paper! and that study is not convicing at all; you have to contrast it to this paper)
• GED: peopel who fail last-chance exam could go on and get GED, so then exclusion restriction might be violated; not the case since percentage of people taking GED very low and not significant (there is graph showing discontinuity for GED, but difference very slow)
• last-chance sample has external validity issue since students who take that exam very different from students who don’t take last-chance exam
• no significant difference between if people report 0 earnings employment for those who pass and those who don’t pass
• for exam question: other paper uses population more similar to full sample, so would be more generalizable, but then has issues that this paper avoided

Question 47

RD 4 - Anderson: Subways, Strikes, and Slowdowns: The Impacts of Public Transit on Traffic Congestion

Answer 47

Issues

• Author uses two models because his results from 2^nd differ from previous literature; to explain difference, argues that commuters that use public transportation are different from car drivers; for that, he uses choice model
  
  • You see this in table 2 – effect for heterogeneous driving speed larger than for homogeneous; could have conducted study with homogeneous, but effect very small then
• Interesting running variable (time, i.e. weeks) which makes this study a before/after comparison; thus, they also could have used DiD (one difference being time (this year with strike compared to next year without strike), another being counties)
• Not accounting for people working at home could lead to underestimation of effect of strike on delay on roads (there might have been more people in streets)
• Bit off to use discontinuity because there is usually no relationship between time and delay, so DiD might have been more appropriate

Question 48

DiD 1 - Rao: Familiarity Does Not Breed Contempt: Generosity, Discrimination, and Diversity in Delhi Schools

Answer 48

• no mistakes

Question 49

DiD 2 - Zölitz: “High” Achievers? Cannabis Access and Academic Performance

Answer 49

• paper only interested in effecct of leaglization, not consumption
• Placebo effect: idea is simply that w/o treatment no effect
• common trend: same trend in test scores, but very different characteristics (more femeale, worse performing), btu same trend so fine
• during treatment period, real difference; find positive effect of strike on test scores; not only for top or bottom, but only bottom
• compositional assumption satisfied (no compositional changes)
• younger students have bigger effect, also females
• two falsification tests
  
  • composition of fellow students (if teacher cna’t buy weed anymore, no effet); same for fellow student
  • placebo tests
    
    • if different treatment timing, doesn’t matter
    • in placebo, standard errors incerase a lot because less clusters
• What they do is ITT, look from policy to outcome but not what happens in between (i.e. maybe fewer students smoke due to other factors)
• major problem: external validity; small percentage of students affected, only look at specific nationalities, age
• Only look at reduced form; why not at IV estimate? Self-report limitations
• How is placebo test different from model: now nationality=1 if Belgian and 0 if DGB
• complaince low since still can buy through dealers (shops are closed); thus see their effect as lower bound since effect would be even larger people if could actually not buy weed
• Why so much less precise in table 7 than in table 4? Clustered at nationality level; clustering allows for intergroup correlation of errors; students are not really clustered at the university in any important regard (don’t have lot in common), so isn’t so clear if you want to do clustering here; this reduces # of observations by a lot; if observations of class are perfectly correlated, only need to observe one; not perfectly correlated, but information I get from additional student in group is not much; so if have low number of clusters, can’t really use clustering; usually want 50+ clusters; if no clustering, standard error would be much smaller, so would be significant, so then would run placebo test that invalidates your findings
  
  • In the experiment there is no real reason to clustering in either table 4 or table 7, so probably still find difference between table 4 and 7 that does not invalidate the finding
  • In their do-file, have a line that says that if a student does not have a nationality, they are not DGB – this is strange, would usually kick those observations out
• in equation 1, the interaction term is capturing the DiD
  
  • nationality variable shows difference between left hand axis and right hand axis (i.e. scaling)
  • discrimination is trend that happens in absence of treatment
• equation 2 does not have nationality anymore because captured in student fixed effects
• initially cluster at nationality level>50, so ok

Question 50

DiD 4 - Arteaga: The effect of human capital on earnings: Evidence from a reform at Colombia’s top university

Answer 50

• comparing economics and business majors in Los Andes to other top universities; common trend must be between those two groups
  
  • main point about common trend: dependent variable is in log wages, so not capturing verying in common trend assumption if looking at log (common trend in logs doesn’t mean common trend in levels)
    *

Question 51

DiD 3 - Field: Entitled To Work: Urban Property Rights And Labor Supply In Peru

Answer 51

• Method
  
  • 1^st diff: squatters and non-squatters (squatters are those that don’t have property rights)
  • 2^nd diff: roll-out of treatment (some people had been treated for longer time, some just had been treated)
  • Don’t have panel, don’t have repeated cross-section, but can still do DiD
• for 200 households, could link data to other data set, so for those had panel data
• antcipation: hosueholds can anticipate that they will have property rights, so might work less just before entitled to property, then effects overestimated - this is Ashton Falter’s dip
  
  • There is no evidence that future program timing has an impact on preprogram labor supply
• in treated nieghborhods, if overall proerty rights go up, so neighborhood will be safer, btu also could argueother way round: now number of households with property rights is smaller
• IV vs ITT: ITT is whole squatter population, IV only at those who got property rights
• table 2: last colmn is DiD
• key assumption: pre-program difference in labor supply between squatters and non-squatters constant across program and nonprogram neighborhoods
• beforehand very difficult to get property rights, after very easy to get them for everyone
• spillover (i.e. violation of compositional changes)? so do people move from untreated neighborhood to treated
• control groups are the same for IV and ITT, treatment gorup different: ITT includes all people in treated neghborhoods, IV only the ones who acutally take up treatment

Question 52

Bounds 1 - Chen, Persson, Polyakova: The Roots Of Health Inequality And The Value Of Intra-Family Expertise

Answer 52

• Method 2 (lottery) not based on many observations
• Table 3: standard errors are high in column 3, most likely due to low number of observations; most individua health indicators not significant, so not very strong evidence
• Preventive health in table 3: might be bad control since condition on specific disease, i.e. conditioning on an outcome; if not conditioning, then mixed results (using more might indicates bad health, but also more complying, i.e. taking medicine, so might be positive effect)
• Evidence materializes very quickly, i.e. doctor still in school and already effect
• Method 3: look at what happens to you in a specific year, controlling for personal fixed effects
  
  • If student goes to medical school, not law school, effect is kappa and sigma
  • Common trend assumption: whatever happens to family members of lawyers is what would have happened to family members of doctors if their nephew would not have gone to medical school
  • You probably know that your nephew is going to med school, so could be anticipation effect (usually in event studies you look at events without anticipation effect); anticipation effect here is a bit far-fetched – would be that you take less care of yourself since soon doctor in family
  • Time is measured in two ways here: t is calendar year, tau is years since person has been in med school; this is assuming that sigmatau does not change over cohorts, so for first person whose health I observe now because nephew started school ten years ago, the health now is same as effect 20 years ago; treatment effect is not different for various cohorts (so idea that med school does not get better with time so that future cohorts would have better education)
• Take OLS with grain of salt – assumptions very strong; lottery – not many observations; method 3 seems solid(?)
• Professor also made a study on similar topic – maybe look at for exam
  
  • Table 5: correlational only, don’t use lottery here yet
  • Strong first stage – coefficient not 1 because many people don’t use the lottery
  • Effects on parental health basically 0
  • This contradicts the conclusions of the other paper, not so much the findings since they also don’t find so much (but conclude significant effect); however, event study effects are positive (mostly due to parents of students at med school different from parents of students at law school)
• Assumptions in paper
  
  • Common trend (would this also be an assumption on DiD?)
  • No anticipation – has typically effect on outcomes (even if there is anticipation, should just not have effect on outcomes)
• bad control: all drugs prescribed; in order to have them, need to be prescribed to you, but in order to get prescription need to be in bad health, so that is bad control
• even study: allow for time of treamtent to vary for people, should be the same across cohorts (this is not likely here with health outcomes)
• event study: my before and after might be different from your before and after; this is the key difference to DiD, where timings are fixed
• complier if win first lottery and become doctor
• people who dont get lottery first time,but go through it again mltiple times are either always takers or defiers; these are differnt from compliers (much more persistent / stubbron), so taht could effect results

Question 53

Bounds 2 - Bindler, Ketel: Scaring or scarring? Labour market effects of criminal victimisation

Answer 53

• Conditioning on victimised individuals – what effect does that have?
• Multiple victimisation and criminal record could be bad controls
• Other methods for this?
  
  • Propensity matching – relies on observable characteristics but unobservables seem to be important here
• Pre-trends biggest issue here
  
  • There are pre-trends, suggest that other things were already going on; they argue here that those people were already victims, but of offenses that were not reported (however there might be other things at work here that effect my labor market outcome and my victimization)
  • The fact that assault effect goes down makes it more credible (people should recover from assault)
• spillover effects shouldn’t matter (if I get violent threat, why would partner labor market outcomes be effected?)
• because of evidence of pre-trend, would assume that assault would behave according to trend, however, seems to not follow it (see “Remarks” slide)
• timing of victimization is not random

Question 54

Bounds 3 - de Haan: The Effect of Parents’ Schooling on Child’s Schooling: A Nonparametric Bounds Analysis

Question 55

IV - which IV assumptions have to hold for reduced form?

Answer 55

• only need independence assumption to be able to conclude sth from this regression (not exclusion, relevance, monotonicity – these are only important from IV perspective)
• random note: IV estimate is reduced form coefficient divided by first stage estimate

Question 56

IV - sometimes SS is not reported - why?

Answer 56

• Might not be precise enough
• Can estimate RF with only one assumption, need more assumptions for SS (including exclusion, which is hard to prove)

Question 57

Regression - Oster

Answer 57

• We know w (observable controls), but not W (unobservable controls)
• delta: to what extent unobservables are important (if 1, selection on unobservables equally important as observables)
• In equation at bottom, chose either delta or R_max (R_max could assume that it’s 1; for delta, 1 is also conservative estimate)
• For covariance equation: LHS tells us sth about observables, RHS about unobservables (if delta is more than one, than selection on unobservables stronger than observables)
• See this approach in situations where you don’t have IVs sets (include as many observables as we can, then see how much beta moves from specification to specification (hopefully not much) and how R² moves (hopefully much)
• Don’t need to know formula by hard, just understand

Question 58

DiD design

Answer 58

• Two groups: treatment group (g = A) and control group (g = B)
• Two time periods: Before (t = 0) and after (t = 1)
• Common trend assumption: In absence of intervention employment in NJ would have had same downward trend as PA
• Two wrong ways to measure treatment effect
  
  • Compare outcomes of treated and controls after intervention (real treatment effect is beta, but end up with beta + (difference between group effect of A minus B); only ok if random assignment, i.e. if groups are the same thus group effect A – group effect B = 0
  • Comparing outcomes or treated before and after treatment: end up with beta + (time effect before – time effect after)
• Thus, subtract diff from diff

Question 59

DiD design - regression

Answer 59

Question 60

DiD - correlation between residuals within a group-time period

Answer 60

Question 61

DiD - serial correlation

Answer 61

Question 62

DiD - common trend assumption

Answer 62

• Key identifying assumption: common trend assumption: In absence of the intervention the treatment and control group(s) should have common trends in the outcome variable
• In principle assumption is untestable, especially with 2 time periods
• With multiple time periods there is a testable implication: investigate pre-intervention trends
• Potential solutions when common trend assumption is unlikely to hold:
  
  • Include time varying covariates and/or group specific time trends
  • Difference-in-difference-in-differences
  • Synthetic control group approach
  • Difference-in-differences + IV approach
  • Changes-in-Changes (nonlinear dif-in-dif)

Question 63

DiD - Ashenfelter’s Dip

Answer 63

• Well known reason for violation of common trend assumption: “Ashenfelter’s Dip”
• Ashenfelter (1978) was first to note that enrollment in a training programme is more likely if temporary dip in earnings occurs just before start of programme
• As a consequence earnings growth after enrollment likely different for participants even without treatment
• Heckman & Smith (1999) investigate earnings growth for randomized-out participants of Job Training Partnership Act programme.
• They show that randomized-out participants show larger earnings growth than nonparticipants
• Due to this violation of common trend assumption DID estimator overestimates effect of treatment.

Question 64

DiD - solutions if common trend assumption doesn’t hold: Time varying covariates and/or group specific time trends

Answer 64

Question 65

DiD - solutions if common trend assumption doesn’t hold: DiDiD

Answer 65

• Sometimes third difference might work when you suspect violation of common trend
• For example: a state implements change in health care policy for people 65 and older
• Possible DID 1: data on health in treatment state before and after, for people >=65 & for people <65 (control group)
  
  • violation common trend: different trends between old & young people
• Possible DID 2: data on health before and after, for people >=65 in treatment state & in neighboring state (control group)
  
  • violation common trend: two states might have different trends
• Possible DiDiD:
  
  • perform DID in treatment state with people <65 as control group
  • perform same DID for control state
  • Difference-in-Difference-in-Differences:
    
    • DID_{treatment state} - DID_{control state}

Question 66

DiD - solutions if common trend assumption doesn’t hold: synthetic control

Answer 66

• formula measures difference between outcome of Miami (Yg1) and the other cities for. All the years up to T (when treatment hits)
  
  • Choose cities similar to Miami in pre-trend, then estimate waits for them based on their similarity (meaning even cities very different to Miami are included, but might receive very little weight)
• 2nd slide: do placebo studies on each state (create a synthetic Colorado, NY etc.) and see what the outcomes would be; non of the 19 states as extreme as California, so probability of estimated effect as large as Calirfornia -effect underrandom permutation of intervention is 5%; this is for standard errors and sampling variation
  
  • Use Placebo test as if sth happened in another state, would we have gotten the same conclusion? Do that for many and thus see how etreme the finding it; shows that this is a chance finding; if we had many findings below California, then would be likely that our finding got by chance
  • Need standard errors here beause we might have sampling variation (selection of states)

Question 67

DiD - solutions if common trend assumption doesn’t hold: DiD and IV

Answer 67

see lecture slides

Question 68

DiD - solutions if common trend assumption doesn’t hold: changes in changes

Answer 68

see slides

Question 69

monotone instrumental variables

Answer 69

• parents (treatment) and grandparents (IV)
  
  • assume that child of parent has higher education than child of parents that have less education
• child’s evel of schooling weakly incerases as function of mother’s level of schooling
• with MTS, look within level (mothers education =1), with MIV look across levels (mothers edcuation = 1,2,3…); look at graph to understand what this means in graph
• can’t compute MIV